题目内容
线段AB所在直线为x+y-2=0,线段AC所在直线为x-7y-4=0,点BC分别在第一、三象限,则角ABC的角平分线的方程为 .
考点:两直线的夹角与到角问题
专题:直线与圆
分析:易得直线的斜率和A的坐标,进而由到角公式可得角平分线的斜率,可得直线的点斜式方程,化为一般式即可.
解答:
解:由题意易得直线AB的斜率为k1=-1,直线AC的斜率为k2=
,
联立方程组
,解得
,即A(
,-
),
设角ABC的角平分线的斜率为k,
则由到角公式可得
=
,解得k=3,或k=-
(舍去),
∴所求直线的方程为y+
=3(x-
),化为一般式可得3x-y-7=0
故答案为:3x-y-7=0
| 1 |
| 7 |
联立方程组
|
|
| 9 |
| 4 |
| 1 |
| 4 |
设角ABC的角平分线的斜率为k,
则由到角公式可得
| k-(-1) |
| 1+k(-1) |
| ||
1+
|
| 1 |
| 3 |
∴所求直线的方程为y+
| 1 |
| 4 |
| 9 |
| 4 |
故答案为:3x-y-7=0
点评:本题考查两直线的到角问题,涉及直线的一般式方程的求解,属基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
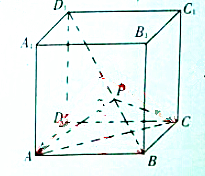
如图,已知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P-ABC的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
点M(1,1),点N(4,5),则|MN|=( )
| A、1 | B、2 | C、3 | D、5 |
已知函数f(x)是定义在R上的函数且满足f(x+
)=-f(x),若x∈(0,3)时,f(x)=log2(3x+1),则f(2011)=( )
| 3 |
| 2 |
| A、4 |
| B、-2 |
| C、2 |
| D、log27 |