题目内容
4.若关于x的不等式xex-2ax+a<0的非空解集中无整数解,则实数a的取值范围是( )| A. | [$\frac{2}{5{e}^{2}}$,$\frac{1}{3e}$) | B. | [$\frac{1}{3e}$,$\frac{\sqrt{e}}{4e}$) | C. | [$\frac{1}{3e}$,e] | D. | [$\frac{\sqrt{e}}{4e}$,e] |
分析 设g(x)=xex,f(x)=2ax-a,求出g(x)的导数,判断直线恒过定点,设直线与曲线相切于(m,n),求得切线的斜率和切点在直线上和曲线上,解方程可得a,再由题意可得当x=-1时,求得a,通过图象观察,即可得到a的范围.
解答 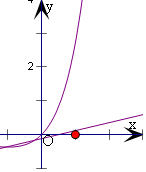 解:设g(x)=xex,f(x)=2ax-a,
解:设g(x)=xex,f(x)=2ax-a,
由题意可得g(x)=xex在直线f(x)=2ax-a下方,
g′(x)=(x+1)ex,
f(x)=2ax-a恒过定点($\frac{1}{2}$,0),
设直线与曲线相切于(m,n),
可得2a=(m+1)em,mem=2am-a,
消去a,可得2m2-m-1=0,解得m=1(舍去)或-$\frac{1}{2}$,
则切线的斜率为2a=(-$\frac{1}{2}$+1)e${\;}^{-\frac{1}{2}}$,
解得a=$\frac{1}{4\sqrt{e}}$,
又由题设原不等式无整数解,
由图象可得当x=-1时,g(-1)=-e-1,f(-1)=-3a,
由f(-1)=g(-1),可得a=$\frac{1}{3e}$,
由直线绕着点($\frac{1}{2}$,0)旋转,
可得$\frac{1}{3e}$≤a<$\frac{1}{4\sqrt{e}}$,
故选:B.
点评 本题考查不等式解法问题,注意运用数形结合的方法,结合导数的运用:求切线的斜率,以及直线恒过定点,考查运算能力和观察能力,属于中档题.

练习册系列答案
相关题目
15.某校卫生所成立了调查小组,调查“按时刷牙与不患龋齿的关系”,对该校某年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:按时刷牙且不患龋齿的学生有160 名,不按时刷牙但不患龋齿的学生有100 名,按时刷牙但患龋齿的学生有 240 名.
(1)该校4名校卫生所工作人员甲、乙、丙、丁被随机分成两组,每组 2 人,一组负责数据收集,另一组负责数据处理,求工作人员甲乙分到同一组的概率.
(2)是否有99.9%的把握认为该年级学生的按时刷牙与不患龋齿有关系?
附:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(1)该校4名校卫生所工作人员甲、乙、丙、丁被随机分成两组,每组 2 人,一组负责数据收集,另一组负责数据处理,求工作人员甲乙分到同一组的概率.
(2)是否有99.9%的把握认为该年级学生的按时刷牙与不患龋齿有关系?
附:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
19.某种电路开关闭合后会出现红灯或绿灯闪烁,已知开关第一次闭合后出现红灯的概率为$\frac{1}{2}$,两次闭合后都出现红灯的概率为$\frac{1}{5}$,则在第一次闭合后出现红灯的条件下第二次闭合后出现红灯的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |