题目内容
已知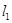 、
、 、
、 是空间三条不同的直线,下列命题中正确的是( )
是空间三条不同的直线,下列命题中正确的是( )
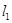 、
、 、
、 是空间三条不同的直线,下列命题中正确的是( )
是空间三条不同的直线,下列命题中正确的是( )A.如果 , , .则 .则 . . |
B.如果 , , .则 .则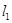 、 、 、 、 共面. 共面. |
C.如果 , , .则 .则 . . |
D.如果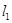 、 、 、 、 共点.则 共点.则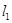 、 、 、 、 共面. 共面. |
A
试题分析:
 ,
, ,则则
,则则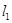 、
、 、
、 可能共面也可能不共面,如三棱柱的三条侧棱;直线的垂直不具备传递性,所以C错误;
可能共面也可能不共面,如三棱柱的三条侧棱;直线的垂直不具备传递性,所以C错误;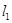 、
、 、
、 共点也可能异面,如三棱锥的三条侧棱,所以D错误,只有A正确.
共点也可能异面,如三棱锥的三条侧棱,所以D错误,只有A正确.点评:考查空间中直线、平面之间的位置关系,要紧扣相关的判定定理和性质定理,定理中要求的条件要缺一不可.

练习册系列答案
相关题目
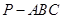 中,
中,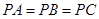 ,
,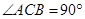 ,
,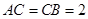 .
. 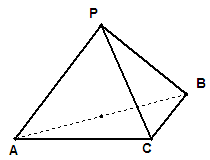
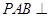 平面
平面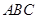 ;
;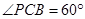 时,求三棱锥
时,求三棱锥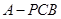 的体积.
的体积. 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, .
. 于点
于点 ,
, 是
是 中点.
中点.
 ⊥平面
⊥平面 ;
;  与平面
与平面 所成的角的正弦值;
所成的角的正弦值;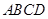 ⊥平面
⊥平面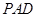 ,
,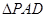 是直角三角形,
是直角三角形,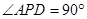 ,四边形
,四边形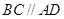 ,
,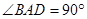 ,
,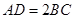 ,且
,且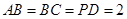 ,
,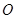 是
是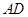 的中点,
的中点,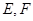 分别是
分别是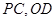 的中点.
的中点. 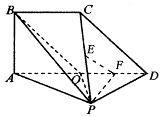
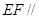 平面
平面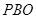 ;
;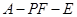 的正切值.
的正切值. 平面ABCD,
平面ABCD, ,BC=1,E为CD的中点,PC与平面ABCD成
,BC=1,E为CD的中点,PC与平面ABCD成 角。
角。
 中,
中, 点为棱
点为棱 的中点.
的中点.
 .
. ,求异面直线
,求异面直线 与
与 所成的角的余弦值.
所成的角的余弦值. ,已知在四棱锥
,已知在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, 是
是 的中点,
的中点,  是线段
是线段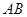 上的点.
上的点.
 平面
平面 ;
; 的大小为
的大小为 ,试确定
,试确定 与
与 均为菱形,
均为菱形,  ,且
,且 ,
,
 平面
平面 ;
; 的余弦值。
的余弦值。 是直线,
是直线, ,
, 是两个不同的平面,下列选项正确的是( )
是两个不同的平面,下列选项正确的是( ) ⊥
⊥