题目内容
若sinα,cosα是方程3x2+6mx+2m+1=0的两根,则实数m的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由题意,利用根与系数的关系表示出sinα+cosα与sinαcosα,再利用同角三角函数间基本关系化简,求出m的值即可.
解答:
解:∵sinα,cosα是方程3x2+6mx+2m+1=0的两根,
∴△=36m2+12(2m+1)=12(3m2+2m+1)≥0,
且sinα+cosα=-
=-2m,sinαcosα=
,
∵(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+2sinαcosα,
∴4m2=1+
,
解得:m=-
或m=
,
当m=
时,sinα+cosα=-
,不成立,舍去;
则m=-
.
故选:A.
∴△=36m2+12(2m+1)=12(3m2+2m+1)≥0,
且sinα+cosα=-
| 6m |
| 3 |
| 2m+1 |
| 3 |
∵(sinα+cosα)2=sin2α+cos2α+2sinαcosα=1+2sinαcosα,
∴4m2=1+
| 4m+2 |
| 3 |
解得:m=-
| 1 |
| 2 |
| 5 |
| 6 |
当m=
| 5 |
| 6 |
| 5 |
| 3 |
则m=-
| 1 |
| 2 |
故选:A.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x的值为( )


| A、1 | B、-2 |
| C、1或-1 | D、1或-2 |
方程lnx+2x-8=0的实数根的个数是( )
| A、0 | B、1 | C、2 | D、3 |
如果f(x)为偶函数,满足在区间[2,3]上是增函数且最小值是4,那么f(x)在区间[-3,-2]上是( )
| A、增函数且最小值是-4 |
| B、增函数且最大值是4 |
| C、减函数且最小值是4 |
| D、减函数且最大值是-4 |
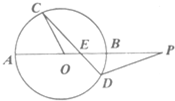 如图;圆O的割线PA过圆心O交圆于另一点B,弦CD交OB于点E,且△COE~△POE,PB=OA=2,则PE的长等于( )
如图;圆O的割线PA过圆心O交圆于另一点B,弦CD交OB于点E,且△COE~△POE,PB=OA=2,则PE的长等于( )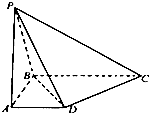 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.