题目内容
在数列{an}中,a1=2,an+1=3an+2,
(1)求数列{an}的通项公式;
(2)求数列an的前n项和Sn.
(1)求数列{an}的通项公式;
(2)求数列an的前n项和Sn.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)利用待定系数法和题意,构造等比数列{an+1},由等比数列的通项公式求出an;
(2)根据分组求和法、等比数列的前n项和公式,求出数列{an}的前n项和Sn.
(2)根据分组求和法、等比数列的前n项和公式,求出数列{an}的前n项和Sn.
解答:
解:(1)设an+1+k=3(an+k)(k是常数),则an+1=3an+2k,
因为an+1=3an+2,所以2k=2,解得k=1,
则an+1+1=3(an+1),即
=3,
又a1=2,则a1+1=3,
所以数列{an+1}是以3为首项、公比的等比数列,
则an+1=3•3n-1=3n,所以an=3n-1;
(2)由(1)得,
数列{an}的前n项和Sn=3+32+33+…+3n-n
=
-n=
.
因为an+1=3an+2,所以2k=2,解得k=1,
则an+1+1=3(an+1),即
| an+1+1 |
| an+1 |
又a1=2,则a1+1=3,
所以数列{an+1}是以3为首项、公比的等比数列,
则an+1=3•3n-1=3n,所以an=3n-1;
(2)由(1)得,
数列{an}的前n项和Sn=3+32+33+…+3n-n
=
| 3(1-3n) |
| 1-3 |
| 3n+1-2n-3 |
| 2 |
点评:本题考查了等比数列的通项公式、前n项和公式,待定系数法构造等比数列,以及分组求和法求数列的前n项和,这是常考的题型.

练习册系列答案
相关题目
9
-(-10)0+(log2
)•(log
2)的值等于( )
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| A、-2 | B、0 | C、8 | D、10 |
 如图,设O为?ABCD所在平面外任意一点,E为OC的中点,若
如图,设O为?ABCD所在平面外任意一点,E为OC的中点,若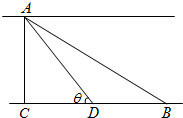 如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.
如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.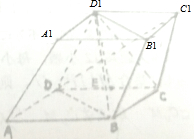 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.