题目内容
14.已知抛物线y2=2px(p>0)与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,若l为双曲线一、三象限的一条渐近线,则l的倾斜角所在的区间可能是( )| A. | $({0,\frac{π}{6}})$ | B. | $({\frac{π}{6},\frac{π}{4}})$ | C. | $({\frac{π}{4},\frac{π}{3}})$ | D. | $({\frac{π}{3},\frac{π}{2}})$ |
分析 根据抛物线和双曲线有相同的焦点求得p和c的关系,根据AF⊥x轴可判断出|AF|的值和A的坐标,代入双曲线方程与p=2c,b2=c2-a2联立求得a和c的关系式,然后求得离心率e,即可得出结论.
解答 解:∵抛物线的焦点和双曲线的焦点相同,
∴p=2c
∵A是它们的一个公共点,且AF垂直x轴,
设A点的纵坐标大于0,
∴|AF|=p,
∴A($\frac{p}{2}$,p),
∵点A在双曲线上,
∴$\frac{{p}^{2}}{4{a}^{2}}-\frac{{p}^{2}}{{b}^{2}}$=1,
∵p=2c,b2=c2-a2,
∴$\frac{{c}^{2}}{{a}^{2}}-\frac{4{c}^{2}}{{c}^{2}-{a}^{2}}$=1,
化简得:c4-6c2a2+a4=0,
∴e4-6e2+1=0,
∵e2>1,
∴e2=3+2$\sqrt{2}$,
∴1+($\frac{b}{a}$)2=3+2$\sqrt{2}$
∴($\frac{b}{a}$)2=2+2$\sqrt{2}$>3
∴l的倾斜角所在的区间可能是($\frac{π}{3}$,$\frac{π}{2}$),
故选:D.
点评 本题主要考查关于双曲线的离心率的问题,属于中档题,本题利用焦点三角形中的边角关系,得出a、c的关系,从而求出离心率.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
4.如图,下列物体的正视图和俯视图中有错误的一项是( )


| A. |  | B. |  | C. |  | D. |  |
6.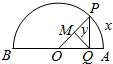 如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )
如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )
 如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )
如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )| A. |  | B. | 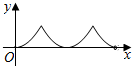 | C. |  | D. | 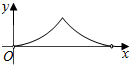 |
3.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=x+x3 | B. | y=3x | C. | y=log2x | D. | $y=-\frac{1}{x}$ |