题目内容
6.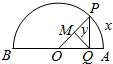 如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )
如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图象是( )| A. |  | B. | 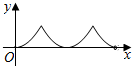 | C. |  | D. | 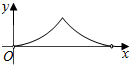 |
分析 在直角三角形OQP中,求出OQ,注意长度、距离为正,再根据直角三角形的锐角三角函数的定义即可得到f(x)的表达式,然后化简,分析周期和最值,结合图象正确选择.
解答 解:在直角三角形OQP中,设OP=1,
∵弧AP的长为x,则∠POQ=x,OQ=|cosx|,
∴点Q到直线OP的距离即QM=y,
∴y=f(x)=OQ|sinx|=|cosx|•|sinx|=$\frac{1}{2}$|sin2x|,
其周期为T=$\frac{π}{2}$,最大值为$\frac{1}{2}$,最小值为0,
故选A.
点评 本题主要考查三角函数的图象与性质,正确表示函数的表达式是解题的关键,同时考查二倍角公式的运用.

练习册系列答案
相关题目
14.已知抛物线y2=2px(p>0)与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,若l为双曲线一、三象限的一条渐近线,则l的倾斜角所在的区间可能是( )
| A. | $({0,\frac{π}{6}})$ | B. | $({\frac{π}{6},\frac{π}{4}})$ | C. | $({\frac{π}{4},\frac{π}{3}})$ | D. | $({\frac{π}{3},\frac{π}{2}})$ |
11.设a>0,b>0.若$\sqrt{3}$是3a与3b的等比中项,则ab的最大值为( )
| A. | 8 | B. | 4 | C. | 1 | D. | $\frac{1}{4}$ |
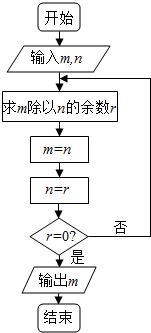 如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )
如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )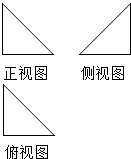 一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )
一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )