题目内容
设函数F(x )=x2+aln(x+1)
(I)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(II)若函数y=f(x)有两个极值点x1,x2且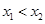 ,求证:
,求证: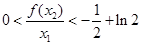 .
.
(I)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(II)若函数y=f(x)有两个极值点x1,x2且
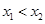 ,求证:
,求证: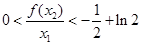 .
.(Ⅰ)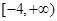 ; (II)见解析.
; (II)见解析.
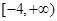 ; (II)见解析.
; (II)见解析.试题分析:(Ⅰ)利用导数,先对函数进行求导,让
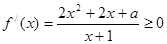 ,在[1,+∞)上是恒成立的,求解可得a的取值范围;(II)令
,在[1,+∞)上是恒成立的,求解可得a的取值范围;(II)令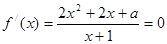 ,依题意方程
,依题意方程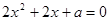 在区间
在区间 有两个不等的实根,记
有两个不等的实根,记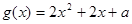 ,则有
,则有 ,得
,得 ,然后找
,然后找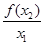 的表达式,利用导数求此函数单调性,可得结论.
的表达式,利用导数求此函数单调性,可得结论.试题解析:(Ⅰ)
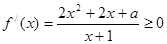 在区间
在区间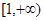 上恒成立,
上恒成立,即
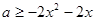 区间
区间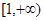 上恒成立, 1分
上恒成立, 1分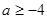 . 3分
. 3分经检验, 当
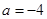 时,
时,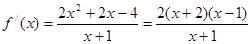 ,
, 时,
时,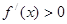 ,
,所以满足题意的a的取值范围为
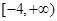 . 4分
. 4分(Ⅱ)函数的定义域
 ,
,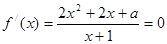 ,依题意方程
,依题意方程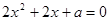 在区间
在区间 有两个不等的实根,记
有两个不等的实根,记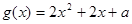 ,则有
,则有 ,得
,得 . 6分
. 6分法一:
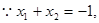
 ,
,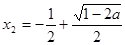 ,
,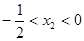 ,
,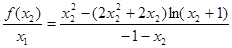 ,令
,令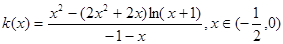 , 8分
, 8分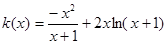 ,
,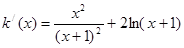 ,
,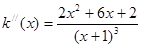 ,
,因为
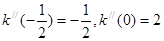 ,存在
,存在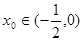 ,使得
,使得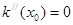 ,
, | 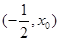 | 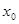 | 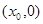 |
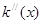 | - | 0 | + |

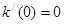 ,
,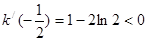 ,
,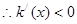 ,所以函数
,所以函数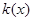 在
在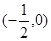 为减函数, 10分
为减函数, 10分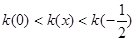 即
即 12分
12分法二:6分段后面还有如下证法,可以参照酌情给分.
【证法2】
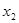 为方程
为方程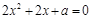 的解,所以
的解,所以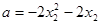 ,
,∵
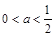 ,
, ,
,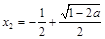 ,∴
,∴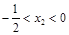 ,
,先证
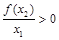 ,即证
,即证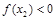 (
( ),
),在区间
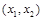 内,
内,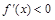 ,
, 内
内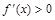 ,所以
,所以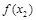 为极小值,
为极小值,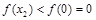 ,
,即
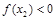 ,∴
,∴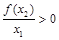 成立; 8分
成立; 8分再证
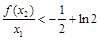 ,即证
,即证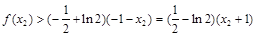 ,
,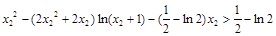 ,
,令
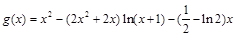 ,
,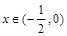 10分
10分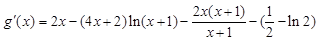 ,
,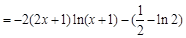 ,
,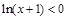 ,
,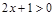 ,
,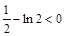 ,
,∴
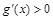 ,
,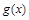 在
在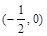 为增函数.
为增函数.
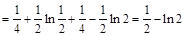 .
.综上可得
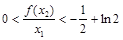 成立. 12分
成立. 12分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
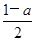
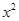 +ax-lnx(a∈R).
+ax-lnx(a∈R).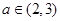 及任意
及任意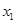 ,
,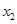 ∈[1,2],恒有
∈[1,2],恒有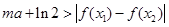 成立,求实数m的取值范围.
成立,求实数m的取值范围.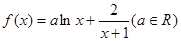 .
.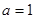 时,求
时,求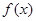 在
在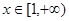 最小值;
最小值;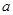 的取值范围;
的取值范围;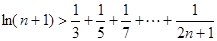 (
(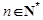 ).
).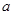 、
、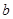 、
、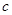 都是实数,函数
都是实数,函数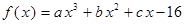 的导函数为
的导函数为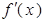 ,
,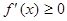 的解集为
的解集为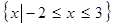 .
.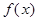 的极大值等于
的极大值等于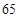 ,求
,求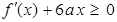 的解集为集合
的解集为集合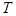 ,当
,当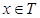 时,函数
时,函数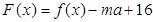 只有一个零点,求实数
只有一个零点,求实数 的取值范围.
的取值范围.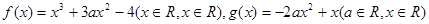 (Ⅰ)若函数
(Ⅰ)若函数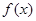 在
在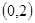 上单调递减,在区间
上单调递减,在区间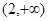 单调递增,求
单调递增,求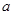 的值;
的值;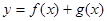 在
在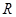 上有两个不同的极值点,求
上有两个不同的极值点,求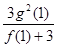 的取值范围;
的取值范围;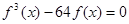 有且只有三个不同的实根,求
有且只有三个不同的实根,求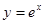 上,点Q在曲线
上,点Q在曲线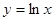 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )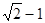
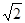

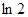
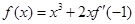 ,则函数
,则函数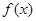 在区间
在区间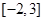 上的值域是_____________.
上的值域是_____________.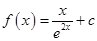 (
(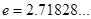 是自然对数的底数,
是自然对数的底数,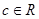 ).
).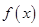 的单调区间、最大值;
的单调区间、最大值;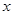 的方程
的方程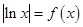 根的个数。
根的个数。 ,记
,记
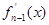 ,
, 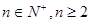 ).则
).则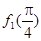 +
+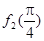 +…+
+…+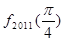 =
=