题目内容
2.若函数f(x)=e|lnx|-|x-1|-($\frac{1}{2}$)m有且仅有一个零点,则实数m的取值范围(-∞,0).分析 把函数f(x)=e|lnx|-|x-1|-($\frac{1}{2}$)m有且仅有一个零点转化为方程e|lnx|-|x-1|=($\frac{1}{2}$)m有且仅有一个根,利用导数研究函数f(x)的单调性,作出其图象的大致形状,数形结合可得($\frac{1}{2}$)m>1,得m<0.
解答 解:函数f(x)=e|lnx|-|x-1|-($\frac{1}{2}$)m有且仅有一个零点,即方程e|lnx|-|x-1|=($\frac{1}{2}$)m有且仅有一个根,
令g(x)=e|lnx|-|x-1|=$\left\{\begin{array}{l}{-elnx+x-1,0<x<1}\\{elnx-x+1,x≥1}\end{array}\right.$,
当0<x<1时,g(x)=-elnx+x-1,得g′(x)=$-\frac{e}{x}+1=\frac{x-e}{x}$<0,g(x)在(0,1)上为减函数;
当x>1时,由g(x)=elnx-x+1,得g′(x)=$\frac{e}{x}-1=\frac{e-x}{x}$,当x∈(1,e)时,g′(x)>0,当x∈(e,+∞)时,g′(x)<0,
∴g(x)在(1,e)上为增函数,在(e,+∞)上为减函数,且g(1)=0,g(e)=1,当x→+∞时,g(x)→-∞.
作出函数g(x)的图象的大致形状如图: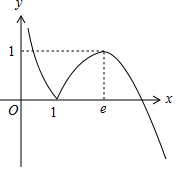
要使方程e|lnx|-|x-1|=($\frac{1}{2}$)m有且仅有一个根,
则($\frac{1}{2}$)m>1,得m<0.
∴m的取值范围为(-∞,0).
故答案为:(-∞,0).
点评 本题考查根的存在性及根的个数判断,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
13.已知函数f(x)=ax-sinx在区间(-$\frac{π}{2}$,$\frac{π}{2}$)上有且仅有一个零点,则a的取值范围是( )
| A. | a≥1 | B. | a≥1或a≤$\frac{2}{π}$ | C. | a>1或a≤0 | D. | a$<\frac{2}{π}$ |
17.已知M={x|y=$\sqrt{1-lo{g}_{2}x}$},N={x|x2-2x-3<0},则M∩N=( )
| A. | (0,2) | B. | (-1,2] | C. | (0,2] | D. | (-1,3) |
7.运行如图算法语句时,执行循环体的次数是( )


| A. | 25 | B. | 4 | C. | 2 | D. | 5 |
12.已知i是虚数单位,复数$\frac{2i}{1+i}$的值为( )
| A. | 1-i | B. | 1+i | C. | i | D. | 2-i |