题目内容
1.已知抛物线x2=4y的焦点F的坐标为(0,1),若M是抛物线上一点,|MF|=4,O为坐标原点,则∠MFO=$\frac{π}{3}$或$\frac{2π}{3}$.分析 利用抛物线的方程与定义,即可得出结论.
解答 解:抛物线x2=4y的焦点在y轴上,且p=1,焦点坐标为(0,1);
∵M是抛物线上一点,|MF|=4,
∴M(±2$\sqrt{3}$,3),
M(2$\sqrt{3}$,3),kMF=$\frac{3-1}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,∴∠MFO=$\frac{π}{3}$
M(-2$\sqrt{3}$,3),kMF=-$\frac{3-1}{2\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$,∴∠MFO=$\frac{2π}{3}$
故答案为:(0,1),$\frac{π}{3}$或$\frac{2π}{3}$.
点评 本题考查抛物线的方程与定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
11.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别为A、B,左右焦点分别为F1、F2,若|AF1|,|F1F2|,|F1B|成等差数列,则此椭圆的离心率为( )
| A. | $\sqrt{5}-2$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
9.从装有2个红球和2个白球的袋内任取两球,下列每对事件中是互斥事件的是( )
| A. | 至少有一个白球;都是白球 | B. | 恰好有一个白球;恰好有两个白球 | ||
| C. | 至少有一个白球;至少有一个红球 | D. | 至多有一个白球;都是红球 |
16.已知平面α与平面β相交于直线l,l1在平面α内,l2在平面β内,若直线l1和l2是异面直线,则下列说法正确的是( )
| A. | l与都相交l1,l2 | B. | l至少与l1,l2中的一条相交 | ||
| C. | l至多与l1,l2中的一条相交 | D. | l与l1,l2都不相交 |
13.定义在(0,+∞)的函数f(x)非负实数,且满足xf′(x)<f(x),若m,n∈(0,+∞)且m<n,则必有( )
| A. | nf(n)<mf(m) | B. | nf(m)<mf(n) | C. | mf(m)<nf(n) | D. | mf(n)<nf(m) |
11.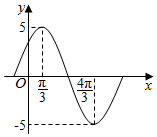 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )| A. | $\frac{3\sqrt{3}+4}{10}$ | B. | $\frac{3\sqrt{3}-4}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |