题目内容
如图,在平行四边形ABCD中,AB=1,BD=![]() ,∠ABD=90°,将它们沿对角线BD折起,折后的C变为C1,且A、C1间的距离为2.
,∠ABD=90°,将它们沿对角线BD折起,折后的C变为C1,且A、C1间的距离为2.
(1)求证:平面A C1D⊥平面ABD;
(2)求二面角B-AC1-D所成角余弦值
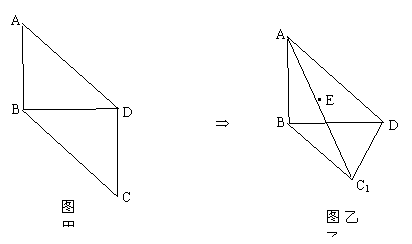
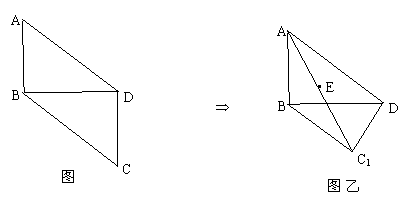 (3)E为线段A C1上的一个动点,当线段EC1的长为多少时?DE与平面BC1D所成的角为30°.
(3)E为线段A C1上的一个动点,当线段EC1的长为多少时?DE与平面BC1D所成的角为30°.
 |
解答:法一:(1)∵ABCD是平行四边形,故知∠BDC1=∠ABD=90°,
即AB⊥BD,C1D⊥BD,
∴ AD=BC1=![]() ,
,
由C1D=1,AC1=2可得,AC12=C1D2+AD2,∴C1D⊥AD.
∴C1D⊥平面ABD,
又C1D Ì平面AC1D,故平面AC1D⊥平面ABD.
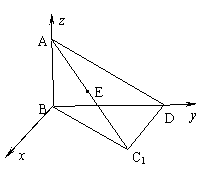
(2)由AB⊥BD,AB⊥C1D可知,AB⊥平面BC1D,故可以B为原点,平行于C1D的直线为x轴建立如图所示的空间直角坐标系.则A(0,0,1),D(0, ![]() ,0),C1(1,
,0),C1(1, ![]() ,0)
,0)
=(0,0,1),=(1, ![]() ,0),=(0,
,0),=(0, ![]() ,-1) ,=(1,0,0).
,-1) ,=(1,0,0).
设平面ABC1的法向量为=(x1,y1,z1),则
·=0,·=0,即
![]() ,解得
,解得![]() ,故得平面ABC1的一个法向量
,故得平面ABC1的一个法向量
=(-![]() ,1,0)……………………
,1,0)……………………
设平面ADC1的法向量为=(x2,y2,z2),则
·=0,·=0,即
![]() ,解得
,解得![]() ,故得平面ABC1的一个法向量
,故得平面ABC1的一个法向量
=(0, 1, ![]() ).
).
∵ ![]() ==
==![]() =
=![]() .
.
显然,二面角B-AC1-D所成的平面角为锐角,故大小为![]() .
.
(3)设=λ,则
=+=+λ=(1,0,0)+λ(-1,-![]() ,1)=(1-λ,-
,1)=(1-λ,-![]() λ, λ),
λ, λ),
由ABC⊥平面BCD可知,=(0,0,1)是平面BCD的一个法向量,
若DE与平面BC1D所成的角为30°,则不难看出
<,>=60°,∴![]()
![]() .
.
又 ![]() =
=![]() .
.
故 ![]() =
=![]() ,整理,得4λ2=1-2λ+4λ2,解得λ=
,整理,得4λ2=1-2λ+4λ2,解得λ=![]() .
.
故知E为AB的中点,即|C1E|=1时.DE与平面BC1D所成的角为30°.
法二:(1)同上.
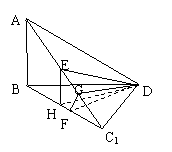
(2)作DF⊥BC1于F,则DF⊥平面ABC1,又作DG⊥AC1,连FG,由三垂线定理可知,则FG⊥AC1,故∠FGD就是二面角B-AC1-D的平面角.
 ∵
∵ ![]() ·B C1·DF=
·B C1·DF=![]() ·BD·D C1,
·BD·D C1,
故 DF=![]() =
=![]() ,
,
同理,DG=![]() =
=![]() =
=![]() .
.
∴ sin∠FGD=![]() =
=![]() ,
,
故二面角B-AC1-D的大小为![]() .
.
(3)过E作EH⊥BC1于H,则EH∥AB,故EH⊥平面BC1D,连DH,则∠EDH就是DE与平面BC1D所成的角.
设|C1E|=x,∵AB=1,AC1=2,故知∠AC1B=30°,则EH=![]() x,
x,
同理可知,∠DC1E=60°,在△DC1E中,由余弦定理得
DE2=12+x2-2·1·x·cos60°=x2-x+1.
若∠EDH=30°,则DE=2EH=x,故有x2=x2-x+1,解得x=1,即|C1E|=1时,DE与平面BC1D所成的角为30°.

 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
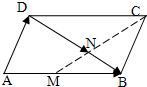 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,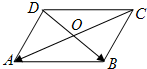 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.