题目内容
19．设随机变量X等可能取1，2，3，…，n这n个值，如果P（X≤4）=0.4，则n等于10．分析 推导出P（X≤4）=P（X=1）+P（X=2）+P（X=3）+P（X=4）=$\frac{1}{n}+\frac{1}{n}+\frac{1}{n}+\frac{1}{n}$=0.4，由此能求出n．
解答 解：∵随机变量X等可能取1，2，3，…，n这n个值，P（X≤4）=0.4，
∴P（X≤4）=P（X=1）+P（X=2）+P（X=3）+P（X=4），
=$\frac{1}{n}+\frac{1}{n}+\frac{1}{n}+\frac{1}{n}$=0.4，
解得n=10．
故答案为：10．
点评 本题考查概率的求法及应用，考查古典概型等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方思想，是基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
9．
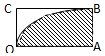如图，长方形的四个顶点坐标为O（0，0），A（4，0），B（4，2），C（0，2），曲线y=$\sqrt{x}$经过点B，现将质点随机投入长方形OABC中，则质点落在图中阴影部分的概率为（ ）
如图，长方形的四个顶点坐标为O（0，0），A（4，0），B（4，2），C（0，2），曲线y=$\sqrt{x}$经过点B，现将质点随机投入长方形OABC中，则质点落在图中阴影部分的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |
10．已知等比数列{an}中的各项都是正数，且${a_1}，\frac{1}{2}{a_3}，2{a_2}$成等差数列，则$\frac{{{a_9}+{a_{10}}+{a_{13}}}}{{{a_7}+{a_8}+{a_{11}}}}$=（ ）
| A． | $1+\sqrt{2}$ | B． | $1-\sqrt{2}$ | C． | $3+2\sqrt{2}$ | D． | $3-2\sqrt{2}$ |
7．将函数f（x）=2sin2x的图象向左平移$\frac{π}{12}$个单位后得到函数g（x）的图象，若函数g（x）在区间[0，$\frac{a}{3}$]和[2a，$\frac{7π}{6}$]上均单调递增，则实数a的取值范围是（ ）
| A． | [$\frac{π}{3}$，$\frac{π}{2}$] | B． | [$\frac{π}{6}$，$\frac{π}{2}$] | C． | [$\frac{π}{6}$，$\frac{π}{3}$] | D． | [$\frac{π}{4}$，$\frac{3π}{8}$] |
4．把函数$y=cos2x+\sqrt{3}sin2x$的图象经过变化而得到y=2sin2x的图象，这个变化是（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{12}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
8．在以下关于向量的命题中，不正确的是（ ）
| A． | 若向量$\overrightarrow a=（x，y）$，向量$\overrightarrow b=（-y，x）$（xy≠0），则$\overrightarrow a⊥\overrightarrow b$ | |
| B． | 若四边形ABCD为菱形，则$\overrightarrow{AB}=\overrightarrow{DC}\;，\;且|\overrightarrow{AB}|=|\overrightarrow{AD}|$ | |
| C． | 点G是△ABC的重心，则$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$ | |
| D． | △ABC中，$\overrightarrow{AB}$和$\overrightarrow{CA}$的夹角等于A |