题目内容
若双曲线的中心在原点,焦点在x轴上,实轴长为12,离心率为
,则双曲线的方程是( )
| 5 |
| 3 |
分析:由题意可得a值,由离心率可得c值,由abc的关系可得b值,代入方程可得.
解答:解:由题意可得2a=12,a=6,离心率e=
=
=
,
解得c=10,故b=
=
=8,
故所求双曲线的方程为:
-
=1
故选D
| c |
| a |
| c |
| 6 |
| 5 |
| 3 |
解得c=10,故b=
| c2-a2 |
| 102-62 |
故所求双曲线的方程为:
| x2 |
| 36 |
| y2 |
| 64 |
故选D
点评:本题考查双曲线的简单性质,涉及a,b的求解,属中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知双曲线的中心在原点,离心率为
.若它的一条准线与抛物线y2=4x的准线重合,则该双曲线与抛物线y2=4x的交点到原点的距离是( )
| 3 |
A、2
| ||||
B、
| ||||
C、18+12
| ||||
| D、21 |
 ,则双曲线的方程是( )
,则双曲线的方程是( ) -
- =1
=1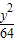 -
-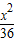 =1
=1 -
- =1
=1 -
-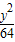 =1
=1