题目内容
7．福州市某家电超市为了使每天销售空调和冰箱获得的总利润达到最大，对某天即将出售的空调和冰箱进行了相关调查，得出下表：| 资金 | 每台空调或冰箱所需资金 （百元） | 每天资金最多供应量 （百元） | |
| 空调 | 冰箱 | ||
| 进货成本 | 30 | 10 | 90 |
| 工人工资 | 5 | 10 | 40 |
| 每台利润 | 2 | 3 | |
分析 设每天调进空调和冰箱分别为x，y台，总利润为 z（百元），建立约束关系，利用线性规划的知识进行求解即可．
解答 解：设每天调进空调和冰箱分别为x，y台，总利润为 z（百元）则由题意，得…．（2分）
则$\left\{\begin{array}{l}{5x+10y≤40}\\{30x+10y≤90}\\{x，y∈N}\end{array}\right.$，化简得$\left\{\begin{array}{l}{x+2y≤8}\\{3x+y≤9}\\{x，y∈N}\end{array}\right.$ …．（6分）
目标函数是z=2x+3y，
…．（9分）
把直线l：2x+3y=0向右上方平移，直线经过可行域上的点M，此时z=2x+3y取最大值
解方程$\left\{\begin{array}{l}{x+2y=8}\\{3x+y=9}\end{array}\right.$得M的坐标为（2，3）…．（11分）
此时最大利润z=2×2+3×3=13百元…．（12分）
答：空调和冰箱的供应量分别为2，3台，总利润为最大，最大为13百元．…．（13分）
点评 本题主要考查线性规划的应用，建立条件，作出图象，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
18．如图，在正六边形ABCDEF中，|$\overrightarrow{AC}$|=2$\sqrt{3}$，则$\overrightarrow{AF}$•$\overrightarrow{FB}$等于（ ）
| A． | -6 | B． | 6 | C． | -2$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
2．
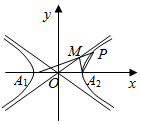设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的顶点为A1，A2，P为双曲线上一点，直线PA1交双曲线C的一条渐近线于M点，直线A2M和A2P的斜率分别为k1，k2，若A2M⊥PA1且k1+4k2=0，则双曲线C离心率为（ ）
设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的顶点为A1，A2，P为双曲线上一点，直线PA1交双曲线C的一条渐近线于M点，直线A2M和A2P的斜率分别为k1，k2，若A2M⊥PA1且k1+4k2=0，则双曲线C离心率为（ ）| A． | 2 | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$ | D． | 4 |
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1，的离心率e=2，若过双曲线右焦点且与渐近线平行的直线与圆x2+y2+4x=8相切，则双曲线的方程为（ ）
| A． | x2-$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
19．等式12+22+32+…+n2=$\frac{1}{2}$（5n2-7n+4）（ ）
| A． | n为任何正整数都成立 | B． | 仅当n=1，2，3时成立 | ||
| C． | 当n=4时成立，n=5时不成立 | D． | 仅当n=4时不成立 |