Question

如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=

2

，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD中点．则异面直线PB与CD所成角的余弦值为（　　）

• A、

  2

  2

• B、

  1

  2

• C、

  6

  3

• D、

  1

  3

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：连结BO，由已知条件得四边形OBCD是平行四边形，推导出∠PBO是异面直线PB与CD所成的角，由此能求出异面直线PB与CD所成的角的余弦值．

解答： 解：连结BO，在直角梯形ABCD中，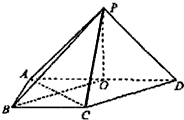
BC∥AD，AD=2AB=2BC，
有OD∥BC且OD=BC，
所以四边形OBCD是平行四边形，
所以OB∥DC
在△PAD中PA=PD，O为AD中点，
所以PO⊥AD
又侧面PAD⊥底面ABCD，平面PAD∩平面ABCD=AD，PO?平面PAD，
所以PO⊥平面ABCD；
所以PO⊥OB，∠PBO为锐角，
所以∠PBO是异面直线PB与CD所成的角
因为AD=2AB=2BC=2，
在Rt△AOB中，AB=1，AO=1，
所以OB=

2

，
在Rt△POA中，因为AP=

2

，AO=1，
所以OP=1，
在Rt△PBO中，PB=

OP2+OB2

=

3

，
cos∠PBO=

OB

PB

=

2

3

=

6

3

，
所以异面直线PB与CD所成的角的余弦值为

6

3

．
故选：C．

点评：本题考查异面直角所成角的余弦值的求法，是中档题，解题时要注意空间思维能力的培养．