题目内容
(选作)求y=e2xcos3x的导数.
解:∵y=e2xcos3x
∴y′=(e2x)′•(cos3x)+(e2x)•(cos3x)′
=2e2xcos3x-3e2xsin3x
分析:由已知中函数的解析式y=e2xcos3x,根据两个函数乘积的导数公式[f(x)•g(x)]′=f′(x)•g(x)+f(x)•g′(x),及复合函数的导数公式f′[g(x)]=f′(u)•u′(x),其中u=g(x),即可得到答案.
点评:本题考查的知识点是导数的运算,其中熟练掌握两个函数乘积的导数公式[f(x)•g(x)]′=f′(x)•g(x)+f(x)•g′(x),及复合函数的导数公式f′[g(x)]=f′(u)•u′(x),其中u=g(x),是解答本题的关键.
∴y′=(e2x)′•(cos3x)+(e2x)•(cos3x)′
=2e2xcos3x-3e2xsin3x
分析:由已知中函数的解析式y=e2xcos3x,根据两个函数乘积的导数公式[f(x)•g(x)]′=f′(x)•g(x)+f(x)•g′(x),及复合函数的导数公式f′[g(x)]=f′(u)•u′(x),其中u=g(x),即可得到答案.
点评:本题考查的知识点是导数的运算,其中熟练掌握两个函数乘积的导数公式[f(x)•g(x)]′=f′(x)•g(x)+f(x)•g′(x),及复合函数的导数公式f′[g(x)]=f′(u)•u′(x),其中u=g(x),是解答本题的关键.

练习册系列答案
相关题目
经过对K2的统计量的研究,得到了若干个临界值,当K2的观测值K>3.841时,我们
| P( K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
- A.在错误的概率不超过0.05的前提下可认为A与B有关
- B.在错误的概率不超过0.05的前提下可认为A与B无关
- C.在错误的概率不超过0.01的前提下可认为A与B有关
- D.没有充分理由说明事件A与B有关
 x3-4x+4
x3-4x+4  ,
, ,
,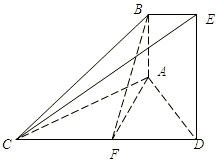 已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AB=1,AD=2,F为CD的中点且AF∥平面BCE.
已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AB=1,AD=2,F为CD的中点且AF∥平面BCE.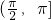 上的函数f(x)=x-sinx,给出下列性质:
上的函数f(x)=x-sinx,给出下列性质: 有相同焦点,且经过点
有相同焦点,且经过点 ,则双曲线的方程为
,则双曲线的方程为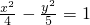
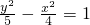


 =(-3,1),
=(-3,1), =(0,5),且
=(0,5),且 ∥
∥ ⊥
⊥ ,则点C的坐标为
,则点C的坐标为 )
)