题目内容
定义在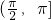
上的函数f（x）=x-sinx，给出下列性质：
①f（x）是增函数；
②f（x）是减函数；
③f（x）有最大值；
④f（x）有最小值．
其中正确的命题是________．
①③
分析：在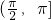上，由y=x和y=-sinx都是增函数，知在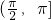上的函数f（x）=x-sinx是增函数．由y=x有最大值π，y=-sinx在x=π处最大值0，知在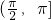上的函数f（x）=x-sinx有最大值．
解答：∵在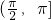上，
y=x和y=-sinx都是增函数，
∴在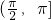上的函数f（x）=x-sinx是增函数．
∵在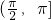上，
y=x有最大值π，y=-sinx在x=π处最大值0，
∴在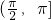上的函数f（x）=x-sinx有最大值．
故答案为：①③．
点评：本题考查函数的单调性和最值的求法，解题时要认真审题，注意三角函数性质的灵活运用．
分析：在
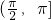上，由y=x和y=-sinx都是增函数，知在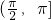上的函数f（x）=x-sinx是增函数．由y=x有最大值π，y=-sinx在x=π处最大值0，知在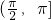上的函数f（x）=x-sinx有最大值．解答：∵在
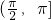上，y=x和y=-sinx都是增函数，
∴在
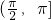上的函数f（x）=x-sinx是增函数．∵在
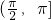上，y=x有最大值π，y=-sinx在x=π处最大值0，
∴在
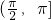上的函数f（x）=x-sinx有最大值．故答案为：①③．
点评：本题考查函数的单调性和最值的求法，解题时要认真审题，注意三角函数性质的灵活运用．
练习册系列答案
相关题目
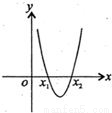
9、方程f（x）=0的根称为函数f（x）的零点，定义在上的函数f（x），其导函数f′（x）的图象如图所示，且f（x1）•f（x2）＜0，则函数f（x）的零点个数是（ ）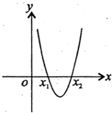
方程f（x）=0的根称为函数f（x）的零点，定义在上的函数f（x），其导函数f′（x）的图象如图所示，且f（x1）•f（x2）＜0，则函数f（x）的零点个数是
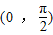上的函数f（x），f′（x）是它的导函数，且恒有f（x）•tanx+f′（x）＜0成立，则（ ）
