题目内容
f(X)= x3-4x+4
x3-4x+4
(1)求函数的极值
(2)求函数在区间(-3,4)上的最大值与最小值.
解:(1)由f(x)= x3-4x+4,得:f′(x)=x2-4.
x3-4x+4,得:f′(x)=x2-4.
由f′(x)=x2-4=0,得:x=-2,或x=2.
列表:

由表可知,函数f(x)的极大值为f(-2)= .
.
函数f(x)的极小值为f(2)= .
.
(2)因为f(-3)= .
.
f(4)= .
.
又f(2)<f(-3)<f(-2),
f(2)<f(4)≤f(-2).
所以,函数f(x)在区间(-3,4)上的最大值为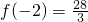 .
.
最小值为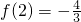 .
.
分析:(1)求出函数f(x)的导函数,解出导函数的零点,由零点对定义域分段,判断导函数在各区间段内的符号,从而得到原函数在各区间段内的单调性,得出极值点,把极值点的横坐标代入原函数解析式求极值;
(2)函数在区间(-3,4)上有一个极大值点和一个极小值点,而x=-3与x=4的函数值都大于该区间内的极小值,小于该区间内的极大值,所以,极小值即为最小值,极大值即为最大值.
点评:本题考查了函数在某点取得极值的条件,连续函数在定义域内某点的两侧的单调性相反,则该点即为函数的极值点,考查了导数在求函数最值时的应用,闭区间上的连续函数一定有最值,开区间内则不一定.此题是中档题.
 x3-4x+4,得:f′(x)=x2-4.
x3-4x+4,得:f′(x)=x2-4.由f′(x)=x2-4=0,得:x=-2,或x=2.
列表:

由表可知,函数f(x)的极大值为f(-2)=
 .
.函数f(x)的极小值为f(2)=
 .
.(2)因为f(-3)=
 .
.f(4)=
 .
.又f(2)<f(-3)<f(-2),
f(2)<f(4)≤f(-2).
所以,函数f(x)在区间(-3,4)上的最大值为
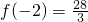 .
.最小值为
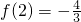 .
.分析:(1)求出函数f(x)的导函数,解出导函数的零点,由零点对定义域分段,判断导函数在各区间段内的符号,从而得到原函数在各区间段内的单调性,得出极值点,把极值点的横坐标代入原函数解析式求极值;
(2)函数在区间(-3,4)上有一个极大值点和一个极小值点,而x=-3与x=4的函数值都大于该区间内的极小值,小于该区间内的极大值,所以,极小值即为最小值,极大值即为最大值.
点评:本题考查了函数在某点取得极值的条件,连续函数在定义域内某点的两侧的单调性相反,则该点即为函数的极值点,考查了导数在求函数最值时的应用,闭区间上的连续函数一定有最值,开区间内则不一定.此题是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目