题目内容
函数f(x)=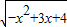 的单调递减区间为( )
的单调递减区间为( )A.(-∞,
 ]
]B.[-1,
 ]
]C.[
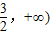
D.[
 ,4]
,4]
【答案】分析:设u(x)=4+3x-x2,则f(x)=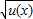 ,因为f(x)=
,因为f(x)=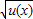 为单调递增函数,要求函数f(x)的减区间只需求二次函数的减区间即可.
为单调递增函数,要求函数f(x)的减区间只需求二次函数的减区间即可.
解答:解:函数f(x)的定义域是[-1,4],
令u(x)=-x2+3x+4,
则u(x)=-(x- )2+
)2+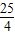 的减区间为[
的减区间为[ ,4],
,4],
又∵f(x)=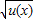 单调递增,
单调递增,
∴函数f(x)的单调减区间为[ ,4].
,4].
故选D.
点评:此题考查学生求幂函数及二次函数增减性的能力,以及判断复合函数增减性的能力,注意单调区间须在定义域内求解.
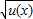 ,因为f(x)=
,因为f(x)=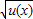 为单调递增函数,要求函数f(x)的减区间只需求二次函数的减区间即可.
为单调递增函数,要求函数f(x)的减区间只需求二次函数的减区间即可.解答:解:函数f(x)的定义域是[-1,4],
令u(x)=-x2+3x+4,
则u(x)=-(x-
 )2+
)2+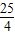 的减区间为[
的减区间为[ ,4],
,4],又∵f(x)=
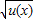 单调递增,
单调递增,∴函数f(x)的单调减区间为[
 ,4].
,4].故选D.
点评:此题考查学生求幂函数及二次函数增减性的能力,以及判断复合函数增减性的能力,注意单调区间须在定义域内求解.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
函数f(x)=|log
x|的单调递增区间是( )
| 1 |
| 2 |
A、(0,
| ||
| B、(0,1] | ||
| C、(0,+∞) | ||
| D、[1,+∞) |