题目内容
函数f(x)=|log
x|的单调递增区间是( )
| 1 |
| 2 |
A、(0,
| ||
| B、(0,1] | ||
| C、(0,+∞) | ||
| D、[1,+∞) |
分析:要求函数的单调递增区间,先讨论x的取值把绝对值号去掉得到分段函数,然后画出函数的图象,在图象上得到增区间.
解答: 解:根据题意得到函数的定义域为(0,+∞),
解:根据题意得到函数的定义域为(0,+∞),
f(x)=|log
x|
当x>1时,根据对数定义得:log
x<0,
所以f(x)=-log
x;当0<x<1时,得到log
x>0,
所以f(x)=log
x.
根据解析式画出函数的简图,
由图象可知,当x>1时,函数单调递增.
故选D
 解:根据题意得到函数的定义域为(0,+∞),
解:根据题意得到函数的定义域为(0,+∞),f(x)=|log
| 1 |
| 2 |
当x>1时,根据对数定义得:log
| 1 |
| 2 |
所以f(x)=-log
| 1 |
| 2 |
| 1 |
| 2 |
所以f(x)=log
| 1 |
| 2 |
根据解析式画出函数的简图,
由图象可知,当x>1时,函数单调递增.
故选D
点评:此题比较好,对数函数加上绝对值后函数的值域发生了变化即原来在x轴下方的图象关于x轴对称到x轴上方了,所以对数函数的图象就改变了,学生这道题时应当注意这一点.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 )2+7lo
)2+7lo +3≤0的解集为M,求当x∈M时,函数f(x)=(lo
+3≤0的解集为M,求当x∈M时,函数f(x)=(lo )(lo
)(lo )的最大值和最小值.
)的最大值和最小值.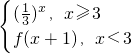 ,则f(2+lo
,则f(2+lo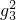 )的值为________.
)的值为________.