题目内容
14.据统计,夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),则在此期间的某一天,该旅游景点的人数不超过1300的概率为( )附:若X~N(μ,σ2),则:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 0.4987 | B. | 0.8413 | C. | 0.9772 | D. | 0.9987 |
分析 根据夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),P(μ-3σ≤X≤μ+3σ)=0.9974,可得(x>1300)=12(1-0.9974)=0.0013,从而可得结论.
解答 解:∵夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),P(μ-3σ≤X≤μ+3σ)=0.9974,
∴P(|x-1000|<300)=0.9974,
∴P(x>1300)=$\frac{1}{2}$(1-0.9974)=0.0013,
∴P(x≤1300)=1-0.0013=0.9987,
故选:D.
点评 一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似的服从正态分布,正态分布在概率和统计中具有重要地位且满足3σ原则.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
14.如图,O为△ABC的外心,AB=4,AC=2,∠BAC为钝角,M是边BC的中点,则$\overrightarrow{AM}$•$\overrightarrow{AO}$的值为( )
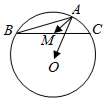

| A. | 4 | B. | 5 | C. | 7 | D. | 6 |
5.若x,y满足不等式组$\left\{\begin{array}{l}{x-y+2>0}\\{x-5y+10≤0}\\{x+y-8≤0}\end{array}\right.$,则z=|x-3|+2y的最小值为( )
| A. | 4 | B. | $\frac{26}{5}$ | C. | 6 | D. | 7 |
2.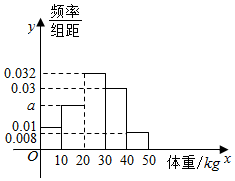 如图为教育部门对辖区内某学校的50名儿童的体重(kg)作为样本进行分析而得到的频率分布直方图,则这50名儿童的体重的平均数为( )
如图为教育部门对辖区内某学校的50名儿童的体重(kg)作为样本进行分析而得到的频率分布直方图,则这50名儿童的体重的平均数为( )
 如图为教育部门对辖区内某学校的50名儿童的体重(kg)作为样本进行分析而得到的频率分布直方图,则这50名儿童的体重的平均数为( )
如图为教育部门对辖区内某学校的50名儿童的体重(kg)作为样本进行分析而得到的频率分布直方图,则这50名儿童的体重的平均数为( )| A. | 27.5 | B. | 26.5 | C. | 25.6 | D. | 25.7 |
9.如果随机变量ξ~N(μ,σ2),Eξ=3,Dξ=1,P(ξ<0)=p,则P(ξ<6)等于( )
| A. | $\frac{1}{2}-p$ | B. | $\frac{1}{2}+p$ | C. | $\frac{1}{2}+\frac{p}{2}$ | D. | 1-p |
19.“m=1”是“复数z=m2+mi-1为纯虚数”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.设i是虚数单位,若复数a-$\frac{17}{4-i}$(a∈R)是纯虚数,则实数a的值为( )
| A. | -4 | B. | -1 | C. | 4 | D. | 1 |
3.设函数f(x)=log${\;}_{\frac{1}{2}}$x+x-a,则“a∈(1,3)”是“函数f(x)在(2,8)上存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
4.在直角坐标平面内,过定点P的直线l:ax+y-1=0与过定点Q的直线m:x-ay+3=0相交于点M,则|MP|2+|MQ|2的值为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | 5 | D. | 10 |