题目内容
5.若x,y满足不等式组$\left\{\begin{array}{l}{x-y+2>0}\\{x-5y+10≤0}\\{x+y-8≤0}\end{array}\right.$,则z=|x-3|+2y的最小值为( )| A. | 4 | B. | $\frac{26}{5}$ | C. | 6 | D. | 7 |
分析 由题意作出其平面区域,化简z=|x-3|+2y=$\left\{\begin{array}{l}{x+2y-3,x≥3}\\{-x+2y+3,x<3}\end{array}\right.$,从而分别求最小值,从而解得.
解答 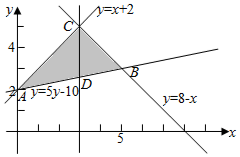 解:由题意作出其平面区域如右图,
解:由题意作出其平面区域如右图,
易知A(0,2),B(5,3),C(3,5),D(3,$\frac{13}{5}$);
z=|x-3|+2y=$\left\{\begin{array}{l}{x+2y-3,x≥3}\\{-x+2y+3,x<3}\end{array}\right.$,
当x≥3时,z=x+2y-3在点D处取得最小值为$\frac{26}{5}$,
当x<3时,z=-x+2y+3>$\frac{26}{5}$,
故z=|x-3|+2y的最小值为$\frac{26}{5}$,
故选B.
点评 本题考查了线性规划的变形应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
相关题目
10.设函数y=f(x)在[a,b]上可导且单调递增,则函数g(x)=$\frac{f(x)-f(a)}{x-a}$在(a,b)上的单调性为( )
| A. | 单调递增 | B. | 单调递减 | C. | 不增不减 | D. | 无法判断 |
10.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( )
| A. | 24里 | B. | 48里 | C. | 96里 | D. | 192里 |
14.据统计,夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),则在此期间的某一天,该旅游景点的人数不超过1300的概率为( )
附:若X~N(μ,σ2),则:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.
附:若X~N(μ,σ2),则:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 0.4987 | B. | 0.8413 | C. | 0.9772 | D. | 0.9987 |
15.若集合A={x∈R|x2<3x},B={x|-1<x<2},则A∪B=( )
| A. | {x|-1<x<0} | B. | {x|-1<x<3} | C. | {x|0<x<2} | D. | {x|0<x<3} |