题目内容
已知数列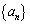 的各项均为正整数,且
的各项均为正整数,且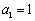 ,
,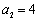 ,
,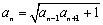 ,
,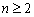 ,
,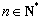 .
.
(1)求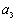 ,
,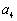 的值;
的值;
(2)求证:对一切正整数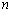 ,
, 是完全平方数.
是完全平方数.
解:(1)由 得,
得, ,
,
由 得,
得, . …………………………2分
. …………………………2分
(2) ,
, ,
, ,
,
猜想: .下面用数学归纳法证明. ……………………5分
.下面用数学归纳法证明. ……………………5分
证明:①当 时,已证;
时,已证;
②假设当 时,
时, 成立,
成立,
那么,当 时,由
时,由 知,
知, ,即
,即 ,
,
又由 知,
知, ,
,
所以 ,
,
所以 ,
,
所以 ,
,
即当 时,命题也成立.
时,命题也成立.
综上可得,对一切正整数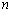 ,
, 是完全平方数.………………………10分
是完全平方数.………………………10分
【思路点拨】(1)把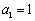 ,
,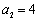 ,代入
,代入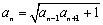 即可. (2)先猜想:
即可. (2)先猜想: .再用数学归纳法证明即可.
.再用数学归纳法证明即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则
,则 的子集中含有元素2的子集共有
的子集中含有元素2的子集共有 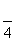 (
(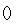 R)对称的曲线的极坐标方程.
R)对称的曲线的极坐标方程. 的公差为
的公差为 ,前
,前 ,且
,且 ,
, ,
, ,
, 的取值范围是 .
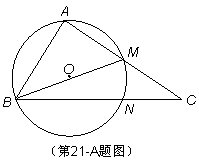
的取值范围是 .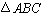 中,
中,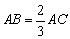 ,
,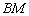 是
是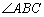 的平分线,
的平分线,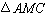 的外接圆交
的外接圆交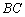 边于点
边于点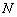 .求证:
.求证: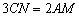 .
.
 的解集与不等式
的解集与不等式 的解集相同,则
的解集相同,则 的值为
的值为 B.
B. C.
C. D.
D. 
 ,则输出的k值为____________.
,则输出的k值为____________.
 ,其中
,其中 表示不小于
表示不小于 的最小整数,如
的最小整数,如 ,
, .当
.当 (
( )时,函数
)时,函数 的值域为
的值域为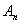 ,记集合
,记集合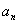 ,则
,则 ________________.
________________.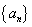 具有如下性质:①
具有如下性质:①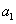 为正整数;②对于任意的正整数
为正整数;②对于任意的正整数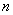 ,当
,当 为偶数时,
为偶数时,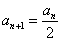 ;当
;当 .在数列
.在数列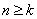 时,
时,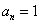 ,当
,当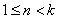 时,
时,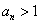 (
(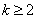 ,
,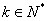 ),则首项
),则首项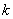 表示)
表示)