题目内容
在如图所示的空间几何体中,平面 平面
平面 ,
, 与
与 是边长为
是边长为 的等边三角形,
的等边三角形, ,
, 和平面
和平面 所成的角为
所成的角为 ,且点
,且点 在平面
在平面 上的射影落在
上的射影落在 的平分线上.
的平分线上.

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
解:(1)由题意知, ,
, 都是边长为2的等边三角形,取
都是边长为2的等边三角形,取 中点
中点 ,连接
,连接 ,则
,则 ,
, ,……………………2分
,……………………2分
又∵平面 ⊥平面
⊥平面 ,∴
,∴ ⊥平面
⊥平面 ,作
,作 ⊥平面
⊥平面 ,
,
那么 ,根据题意,点
,根据题意,点 落在
落在 上,
上,
 ∴
∴ ,易求得
,易求得 ,…………4分
,…………4分
∴四边形 是平行四边形,∴
是平行四边形,∴ ,∴
,∴ 平面
平面 …………6分
…………6分
(2)解法一:作 ,垂足为
,垂足为 ,连接
,连接 ,
,
∵ ⊥平面
⊥平面 ,∴
,∴ ,又
,又 ,
,
∴ 平面
平面 ,∴
,∴ ,∴
,∴ 就是二面角
就是二面角 的平面角.…………9分
的平面角.…………9分
 中,
中, ,
, ,
, .
.
∴ .即二面角
.即二面角 的余弦值为
的余弦值为 .………12分
.………12分
解法二:建立如图所示的空间直角坐标系 ,可知平面
,可知平面 的一个法向量为
的一个法向量为
设平面 的一个法向量为
的一个法向量为
则, 可求得
可求得 .………………9分
.………………9分
所以 ,
,
又由图知,所求二面角的平面角是锐角,所以二面角 的余弦值为
的余弦值为 .……12分
.……12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -
- +
+ -
- +…+
+…+ -
- 的值.
的值. ,下列说法正确的是
,下列说法正确的是 是奇函数且在(
是奇函数且在( )上递增 B.
)上递增 B. )上递增 D.
)上递增 D. ,则二项式
,则二项式 的展开式中
的展开式中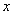 的系数为
的系数为 
 则
则 的最大值是( )
的最大值是( ) (B)
(B) (C)
(C) (D)
(D)
 ,
, ,求
,求 的取值范围;
的取值范围; .
.