题目内容
7．
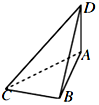如图，在正三棱柱ABC-A1B1C1中，D为棱AA1的中点．若截面△BC1D是面积为6的直角三角形，则此三棱柱的体积为$8\sqrt{3}$．
分析 设AC=a，CC1=b，由截面△BC1D是面积为6的直角三角形列式求出a，b，则三棱柱的体积可求．
解答 解：设AC=a，CC1=b，
截面△BC1D是面积为6的直角三角形，
则由（a2+$\frac{1}{4}{b}^{2}$）×2=a2+b2，
得b2=2a2，又$\frac{1}{2}×\frac{3}{2}{a}^{2}=6$，
∴a2=8，则${S}_{△ABC}=\frac{\sqrt{3}}{4}{a}^{2}$，
∴V=$\frac{\sqrt{3}}{4}×8×4=8\sqrt{3}$，
故答案为$8\sqrt{3}$．
点评 本题考查棱柱的体积的求法，考查计算能力，是中档题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
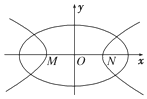如图，中心均为原点O的椭圆与双曲线有公共焦点，M，N是双曲线的两顶点．若M，O，N将椭圆长轴四等分，则椭圆与双曲线的离心率的比值是为$\frac{1}{2}$．
2．复数z=1+3i的模等于（ ）
| A． | 2 | B． | 4 | C． | $\sqrt{10}$ | D． | $2\sqrt{2}$ |
如图所示：有三根针和套在一根针上的若干金属片．按下列规则，把金属片从一根针上全部移到另一根针上：①每次只能移动一个金属片；②在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面．将n根金属片从1号针移到3号针最小需要移动的次数为f（n），则f（10）1023．