题目内容
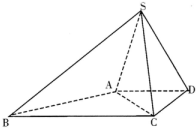 如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=
如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=| 2 |
(I)求证:AC⊥SD;
(Ⅱ)求SB与平面ABCD所成的角的余弦值.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(I)如图所示,作SO⊥平面ABCD,垂足为O点.由SA=SC=SD,可得O点为△ACD的外心.又∠ADC=90°.因此O点为斜边AC的中点.利用线面垂直的判定定理和性质定理即可证明.
(II)连接OB,由(I)可得:∠SBO为SB与平面ABCD所成的角.利用等边三角形的性质可得SO=
.再利用已知可得AB=AC=
,利用勾股定理可得BO,进而得到∠SBO.
(II)连接OB,由(I)可得:∠SBO为SB与平面ABCD所成的角.利用等边三角形的性质可得SO=
| 3 |
| 2 |
解答:
解:(I)如图所示,作SO⊥平面ABCD,垂足为O点.
∵SA=SC=SD,∴O点为△ACD的外心.
∴∠ADC=90°.
∴O点为斜边AC的中点.
∴DO⊥AC,SO⊥AC.
∵SO∩OD=O,
∴AC⊥平面SOD,
∴AC⊥SD;
(II)连接OB,由(I)可得:∠SBO为SB与平面ABCD所成的角.
∵AD=DC=
,∠ADC=90°.
∴∠DAC=45°=∠ACD,AC=2.
∴SO=
.
∵∠BAD=135°,∴∠BAC=90°,
∵BC∥AD,∴∠BCD=90°.
∴∠ACB=45°.
∴AB=AC=2.
∴OB=
=
=
.
∴∠ABC=45°.
∴SB与平面ABCD所成的角为45°.

∵SA=SC=SD,∴O点为△ACD的外心.
∴∠ADC=90°.
∴O点为斜边AC的中点.
∴DO⊥AC,SO⊥AC.
∵SO∩OD=O,
∴AC⊥平面SOD,
∴AC⊥SD;
(II)连接OB,由(I)可得:∠SBO为SB与平面ABCD所成的角.
∵AD=DC=
| 2 |
∴∠DAC=45°=∠ACD,AC=2.
∴SO=
| 3 |
∵∠BAD=135°,∴∠BAC=90°,
∵BC∥AD,∴∠BCD=90°.
∴∠ACB=45°.
∴AB=AC=2.
∴OB=
| AB2+AO2 |
(
|
| 3 |
∴∠ABC=45°.
∴SB与平面ABCD所成的角为45°.
点评:本题考查了线面垂直的判定与性质定理、直角三角形的外心性质、等腰直角三角形与等边三角形的性质,考查了推理能力和计算能力,考查了空间想象能力,属于难题.

练习册系列答案
相关题目