题目内容
设关于x的方程sin(2x+
)=
在[0,
]内有两个不同根α,β,求α+β的值及k的取值范围.
| π |
| 6 |
| k+1 |
| 2 |
| π |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:由于x∈[0,
],可得(2x+
)∈[
,
].由于关于x的方程sin(2x+
)=
在[0,
]内有两个不同根α,β,可得
=sin
≤
<1,α+β=2×
.即可得出.
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| k+1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| k+1 |
| 2 |
| π |
| 2 |
解答:
解:∵x∈[0,
],∴(2x+
)∈[
,
].
∵关于x的方程sin(2x+
)=
在[0,
]内有两个不同根α,β,
∴
=sin
≤
<1,
解得0≤k<1,
∴α+β=2×
=π.
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∵关于x的方程sin(2x+
| π |
| 6 |
| k+1 |
| 2 |
| π |
| 2 |
∴
| 1 |
| 2 |
| π |
| 6 |
| k+1 |
| 2 |
解得0≤k<1,
∴α+β=2×
| π |
| 2 |
点评:本题考查了三角函数的图象与性质,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
 正△ABC的边长为2,CD是AB边上的高,E,F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).在图(2)中:
正△ABC的边长为2,CD是AB边上的高,E,F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).在图(2)中: 如图,已知ABCD是圆锥SO底面圆O的内接矩形.
如图,已知ABCD是圆锥SO底面圆O的内接矩形.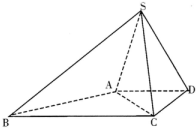 如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=
如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=