题目内容
已知集合A={2,4,6,8,9},B={1,2,3,5,8},是否存在集合C,使C中的每一个元素都加上2变成A的一个子集,且C的每个元素都减去2,就变成了B的一个子集?若存在,求出集合C;若不存在,请说明理由.
考点:子集与真子集
专题:集合
分析:若设集合A中每个元素都减去2变成集合D={0,2,4,6,7},则C⊆D;设集合B中每个元素都加上2变成集合E={3,4,5,7,10},则C⊆E,所以D∩E={4,7}所以C⊆(D∩E),所以集合C便能找到.
解答:
解:若存在集合C,根据已知条件知道:
若设集合A中每一个元素都减去2变成集合D,则D={0,2,4,6,7};
集合B的每一个元素都加上2变成集合E,则E={3,4,5,7,10};
∴D∩E={4,7};
∴C={4},{7},{4,7}.
若设集合A中每一个元素都减去2变成集合D,则D={0,2,4,6,7};
集合B的每一个元素都加上2变成集合E,则E={3,4,5,7,10};
∴D∩E={4,7};
∴C={4},{7},{4,7}.
点评:考查子集的概念,交集的概念,通过已知条件能得到:集合C是集合A中每个元素都减去2所变成集合的子集,集合C是集合B中每个元素都加上2所变成集合的子集是求解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 正△ABC的边长为2,CD是AB边上的高,E,F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).在图(2)中:
正△ABC的边长为2,CD是AB边上的高,E,F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).在图(2)中: 已知函数f(x)=-x2+8x的图象上一点P(1,f(1)),过P作平行于x轴的直线l1,直线l2:x=2,求如图所示的阴影部分的面积S.
已知函数f(x)=-x2+8x的图象上一点P(1,f(1)),过P作平行于x轴的直线l1,直线l2:x=2,求如图所示的阴影部分的面积S.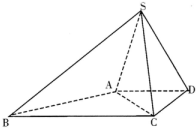 如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=
如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=