题目内容
若
-
=-2tanα,则角α的取值范围是 .
|
|
考点:同角三角函数基本关系的运用,二倍角的正弦
专题:三角函数的求值
分析:已知等式左边变形后,利用同角三角函数间的基本关系化简,确定出α的范围即可.
解答:
解:已知等式变形得:
-
=
-
=
=
=
=-2tanα=
,
∴|cosα|=-cosα,即cosα<0,
则角α的取值范围是{α|
+2kπ<α<
+2kπ,k∈Z}.
故答案为:{α|
+2kπ<α<+
+2kπ,k∈Z}
|
|
| |cosα| |
| 1-sinα |
| |cosα| |
| 1+sinα |
| |cosα|(1+sinα-1+sinα) |
| cos2α |
| 2sinα|cosα| |
| cos2α |
| 2sinα |
| |cosα| |
| -2sinα |
| cosα |
∴|cosα|=-cosα,即cosα<0,
则角α的取值范围是{α|
| π |
| 2 |
| 3π |
| 2 |
故答案为:{α|
| π |
| 2 |
| 3π |
| 2 |
点评:此题考查了同角三角函数基本关系的运用,以及余弦函数的性质,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
若函数y=x2-6x-7,则它在[-2,4]上的最大值,最小值分别是( )
| A、9,-15 |
| B、12,-15 |
| C、9,-16 |
| D、9,-12 |
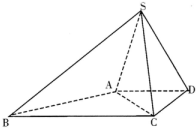 如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=
如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=