题目内容
已知圆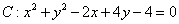 ,
,
(Ⅰ)若过定点(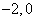 )的直线
)的直线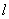 与圆
与圆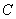 相切,求直线
相切,求直线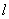 的方程;
的方程;
(Ⅱ)若过定点(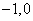 )且倾斜角为
)且倾斜角为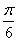 的直线
的直线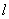 与圆
与圆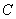 相交于
相交于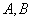 两点,求线段
两点,求线段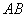 的中点
的中点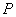 的坐标;
的坐标;
(Ⅲ) 问是否存在斜率为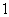 的直线
的直线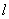 ,使
,使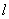 被圆
被圆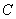 截得的弦为
截得的弦为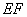 ,且以
,且以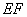 为直径的圆经过原点?若存在,请写出求直线
为直径的圆经过原点?若存在,请写出求直线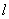 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(Ⅰ)根据题意,设直线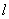 的方程为:
的方程为: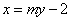
联立直线与圆的方程并整理得: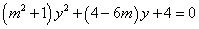 …2分
…2分
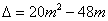 所以
所以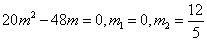
从而,直线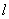 的方程为:
的方程为: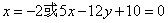 …4分
…4分
(Ⅱ)根据题意,设直线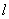 的方程为:
的方程为:
代入圆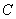 方程得:
方程得: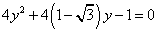 ,显然
,显然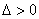 , …6分
, …6分
设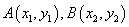 则
则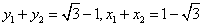
所以点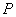 的坐标为
的坐标为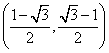 …8分
…8分
(Ⅲ)假设存在这样的直线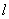 :
: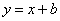
联立圆的方程并整理得: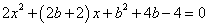
当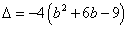
 …9分
…9分
设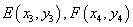 则
则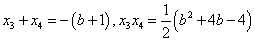
所以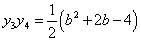 …10分
…10分
因为以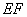 为直径的圆经过原点,所以
为直径的圆经过原点,所以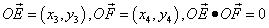
 均满足
均满足 。
。
所以直线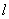 的方程为:
的方程为: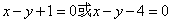 。 …13分
。 …13分
(Ⅲ)法二:可以设圆系方程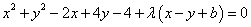
则圆心坐标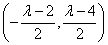 ,圆心在直线
,圆心在直线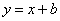 上,且该圆过原点。易得b的值。
上,且该圆过原点。易得b的值。

练习册系列答案
相关题目
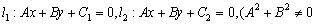 且
且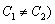 .求证:
.求证: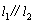 ;
;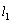 与
与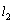 之间的距离是
之间的距离是 .
.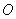 ,焦点为
,焦点为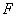 ,
,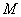 是抛物线上的动点,则
是抛物线上的动点,则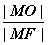 的最大值为 .
的最大值为 .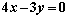 和
和 轴都相切,则该圆的标准方程是( )
轴都相切,则该圆的标准方程是( )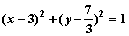 B.
B.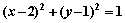
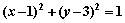 D.
D.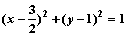
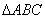 的三个顶点
的三个顶点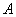 (4,0),
(4,0),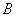 (8,10),
(8,10),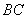 的直线方程;
的直线方程;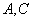 距离相等的直线方程。
距离相等的直线方程。 的前
的前 项和为
项和为 ,若
,若 ,则数列
,则数列 B.1 C.2 D.3
B.1 C.2 D.3 、
、 、
、 成等比数列,且
成等比数列,且 ,若
,若 ,
, 为正常数,则
为正常数,则 B.
B. C.
C. D.
D.
 则
则 是
是 的 ( )
的 ( )