题目内容
已知两条直线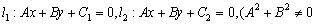 且
且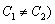 .求证:
.求证:
(1)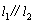 ;
;
(2)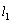 与
与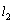 之间的距离是
之间的距离是 .
.
证明:(1)(方法一)若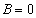 ,则
,则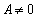 ,
,
所以两条直线变为: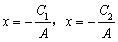 ,
,
所以两条直线都与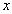 轴垂直,所以
轴垂直,所以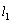
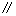
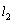 或重合.
或重合.
又由于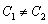 ,所以
,所以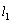
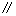
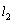 . ……………………………………………………… 2分
. ……………………………………………………… 2分
若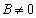 ,则两直线方程化为
,则两直线方程化为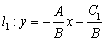 ;
;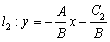 .
.
所以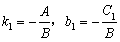 ;
;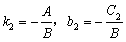 .又
.又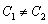 ,
,
所以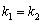 且
且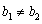 ,即两直线的斜率相等且在
,即两直线的斜率相等且在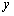 轴上的截距不等,
轴上的截距不等,
所以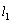
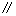
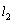 . ………………………………………………………………………… 6分
. ………………………………………………………………………… 6分
(方法二)因为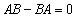 ,所以
,所以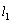
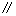
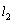 或重合.
或重合.
又因为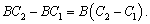
当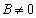 时,因为
时,因为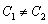 ,所以
,所以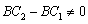 ,因此
,因此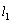
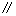
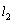 ;………………… 2分
;………………… 2分
当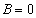 时,
时,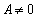 ,所以两条直线变为:
,所以两条直线变为:
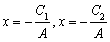 ,
,
所以两条直线都与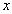 轴垂直,所以
轴垂直,所以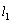
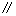
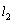 或重合.
或重合.
又由于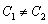 ,所以
,所以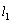
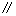
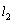 . ……………………………………………………… 6分
. ……………………………………………………… 6分
(2)在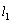 上任取一点
上任取一点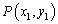 ,则
,则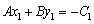 .
.
所以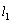 与
与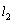 之间的距离等于点
之间的距离等于点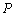 到
到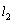 的距离, …………………………………… 9分
的距离, …………………………………… 9分
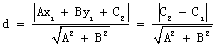 . …………………………………………… 12分
. …………………………………………… 12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
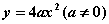 的焦点坐标为
的焦点坐标为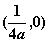 B、
B、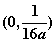 C、
C、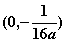 D、
D、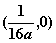
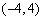 的抛物线的标准方程是 .
的抛物线的标准方程是 .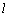 :
: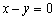 和点
和点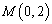 ,则点
,则点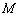 关于直线
关于直线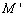 的坐标是( )
的坐标是( )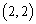 B.
B.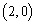 C.
C. D.
D.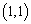
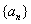 的前n项和为
的前n项和为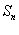 ,且
,且 =6,
=6,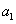 =4, 则公差d等于
=4, 则公差d等于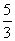 C.- 2 D 3
C.- 2 D 3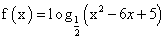 在
在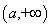 上是减函数,则
上是减函数,则 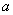 的取值范围是
的取值范围是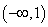 B.
B.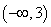 C.
C. 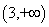 D.
D.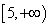
 ,则A∩B的子集的个数是( )
,则A∩B的子集的个数是( )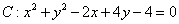 ,
, 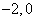 )的直线
)的直线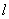 与圆
与圆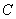 相切,求直线
相切,求直线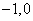 )且倾斜角为
)且倾斜角为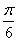 的直线
的直线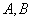 两点,求线段
两点,求线段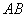 的中点
的中点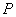 的坐标;
的坐标;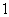 的直线
的直线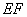 ,且以
,且以