题目内容
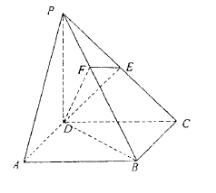
(本小题满分12分)如图所示,平面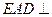 平面
平面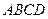 ,
,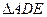 是等边三角形,
是等边三角形,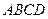 是矩形,
是矩形,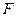 是
是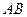 的中点,
的中点,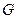 是
是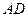 的中点,
的中点,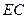 与平面
与平面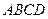 成
成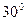 角.
角.
(1)求证: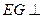 平面
平面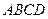 ;
;
(2)若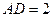 ,求二面角
,求二面角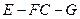 的度数;
的度数;
(3)当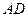 的长是多少时,
的长是多少时, 点到平面
点到平面 的距离为
的距离为 ?并说明理由
?并说明理由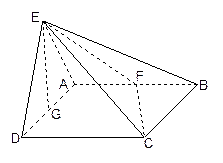
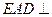 平面
平面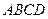 ,
,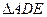 是等边三角形,
是等边三角形,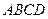 是矩形,
是矩形,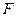 是
是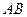 的中点,
的中点,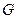 是
是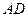 的中点,
的中点,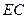 与平面
与平面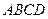 成
成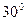 角.
角.(1)求证:
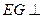 平面
平面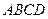 ;
;(2)若
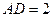 ,求二面角
,求二面角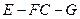 的度数;
的度数;(3)当
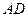 的长是多少时,
的长是多少时, 点到平面
点到平面 的距离为
的距离为 ?并说明理由
?并说明理由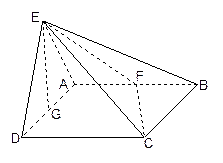
(1)证明见解析
(2)
(3)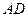 的长为
的长为 时,
时,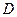 点到平面
点到平面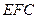 的距离为
的距离为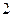
(2)

(3)
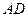 的长为
的长为 时,
时, 点到平面
点到平面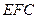 的距离为
的距离为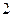
(1)证明.:如图所示,

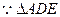 是等边三角形,
是等边三角形,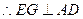
又平面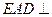 平面
平面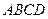 且相交于
且相交于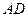 ,
,
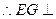 平面
平面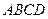 ……………3分
……………3分
(2)连结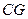 ,则
,则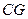 是
是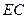 在平面
在平面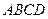 的射影
的射影
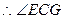 是
是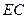 与平面
与平面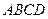 所成的角,
所成的角,
即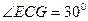
在 中:
中: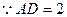 ,
,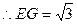 ,
,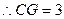
在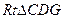 中:
中: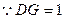 ,
,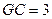 ,
,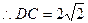
则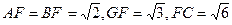
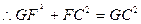 ,即
,即
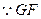 是
是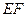 在平面
在平面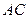 内的射影,
内的射影,
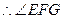 是二面角
是二面角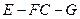 的平面角.
的平面角.
在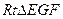 中,
中,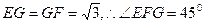 …………………8分
…………………8分
故所求二面角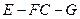 的度数为
的度数为 .
.
(3)连结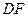 ,
,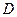 点到平面
点到平面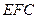 的距离即为三棱锥
的距离即为三棱锥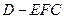 的高.
的高.
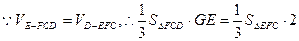
设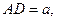 则
则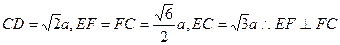 ,则
,则
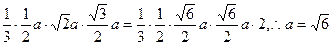
故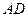 的长为
的长为 时,
时,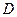 点到平面
点到平面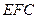 的距离为
的距离为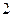 . …………12分
. …………12分
注:本题也可用向量法解决,具体解法略

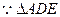 是等边三角形,
是等边三角形,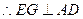
又平面
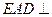 平面
平面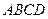 且相交于
且相交于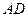 ,
,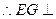 平面
平面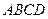 ……………3分
……………3分(2)连结
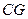 ,则
,则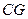 是
是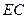 在平面
在平面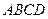 的射影
的射影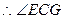 是
是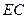 与平面
与平面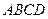 所成的角,
所成的角,即
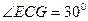
在
 中:
中: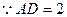 ,
,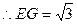 ,
,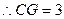
在
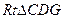 中:
中: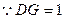 ,
,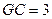 ,
,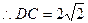
则
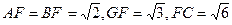
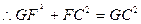 ,即
,即
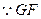 是
是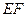 在平面
在平面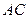 内的射影,
内的射影,
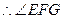 是二面角
是二面角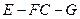 的平面角.
的平面角.在
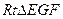 中,
中,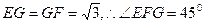 …………………8分
…………………8分故所求二面角
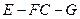 的度数为
的度数为 .
.(3)连结
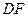 ,
,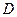 点到平面
点到平面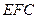 的距离即为三棱锥
的距离即为三棱锥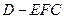 的高.
的高.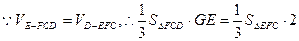
设
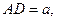 则
则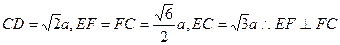 ,则
,则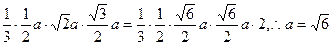
故
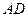 的长为
的长为 时,
时,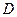 点到平面
点到平面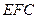 的距离为
的距离为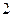 . …………12分
. …………12分注:本题也可用向量法解决,具体解法略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
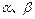 的交线, 已知二面角
的交线, 已知二面角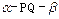 为直二面角,
为直二面角, 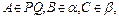
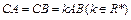 , ∠BAP=45°.
, ∠BAP=45°. 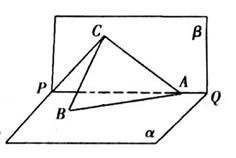
 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心? 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.
 中,底面
中,底面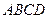 是正方形,侧棱
是正方形,侧棱 ,
, 为
为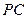 中点,作
中点,作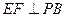 交
交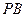 于
于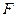
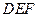 与平面
与平面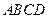 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。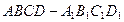 中(侧 棱与底面垂直的四棱柱),
中(侧 棱与底面垂直的四棱柱),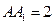 ,底面是边长为
,底面是边长为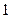 的正方形,
的正方形,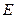 、
、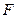 、
、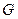 分别是棱
分别是棱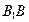 、
、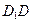 、
、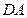 的中点
的中点
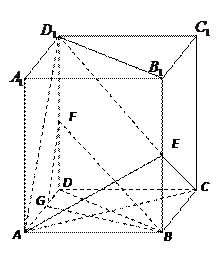
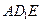
 平面
平面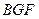 ;
;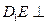 面
面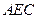 。
。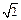 ,AA1=
,AA1=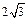 ,求AC1与平面ABC所成的角.
,求AC1与平面ABC所成的角.
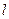 、
、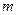 、
、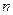 是互不相同的空间直线,
是互不相同的空间直线,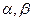 是不重合的平面,则下列命题中为真命题的是( )
是不重合的平面,则下列命题中为真命题的是( )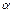 ∥β,
∥β,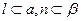 ,则
,则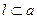 ,则
,则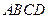 中,
中, 分别是
分别是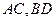 的中点,若
的中点,若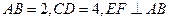 ,
, 与
与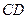 所成的角的大小为。
所成的角的大小为。