题目内容
 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,M是CC1的中点,N是BC的中点,点P为线段A1B1上的动点,
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,M是CC1的中点,N是BC的中点,点P为线段A1B1上的动点,(Ⅰ)判断异面直线PN和AM所成的角的大小是否变化,并证明你的结论;
(Ⅱ)当直线PN和平面ABC所成角最大时,试确定点P的位置.
考点:直线与平面所成的角,异面直线及其所成的角
专题:综合题
分析:(Ⅰ)取AC的中点O,连接A1O,NO,则A1O是PN在平面A1C中的射影,证明AM⊥A1O,即可得出结论;
(Ⅱ)设PD⊥AB,则PD⊥平面ABC,连接DN,则∠PND为直线PN和平面ABC所成角,即可得出结论.
(Ⅱ)设PD⊥AB,则PD⊥平面ABC,连接DN,则∠PND为直线PN和平面ABC所成角,即可得出结论.
解答:
 解:(I)不变;
解:(I)不变;
取AC的中点O,连接A1O,NO,则A1O是PN在平面A1C中的射影,
∵直三棱柱ABC-A1B1C1中,AC=AA1,M是CC1的中点,
∴AM⊥A1O,∴AM⊥PN,
∴异面直线PN和AM所成的角为90°;
(II)设PD⊥AB,则PD⊥平面ABC,连接DN,则∠PND为直线PN和平面ABC所成角,
∴tan∠PND=
,
∴DN最小时,直线PN和平面ABC所成角最大,此时P为A1B1的中点.
 解:(I)不变;
解:(I)不变;取AC的中点O,连接A1O,NO,则A1O是PN在平面A1C中的射影,
∵直三棱柱ABC-A1B1C1中,AC=AA1,M是CC1的中点,
∴AM⊥A1O,∴AM⊥PN,
∴异面直线PN和AM所成的角为90°;
(II)设PD⊥AB,则PD⊥平面ABC,连接DN,则∠PND为直线PN和平面ABC所成角,
∴tan∠PND=
| PD |
| DN |
∴DN最小时,直线PN和平面ABC所成角最大,此时P为A1B1的中点.
点评:本题考查异面直线PN和AM所成的角,考查直线PN和平面ABC所成角最大,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
sin(π+α)=( )
| A、cosα | B、-cosα |
| C、sinα | D、-sinα |
已知M(-c,0),N(c,0),若|PM|-|PN|=c(c>0),则动点P的轨迹是( )
| A、双曲线的左支 |
| B、双曲线的右支 |
| C、以N为端点的射线 |
| D、线段MN |
已知等差数列{an}的公差和首项都不等于0,且a2、a4、a8成等比数列,则下列式子的值最小的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
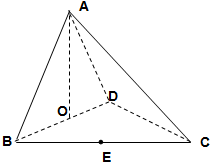 如图,在四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=