题目内容
3.函数y=tan2x-2tanx+3的最小值是2,这时x=$\frac{π}{4}$+kπ,k∈Z.分析 使用配方法,利用二次函数的性质得出最小值,利用正切函数的性质得出x的值.
解答 解:y=tan2x-2tanx+3=(tanx-1)2+2.
∴当tanx=1时,y取得最小值2.
此时x=$\frac{π}{4}+kπ$,k∈Z.
故答案为:2,$\frac{π}{4}+kπ$,k∈Z.
点评 本题考查了正切函数的图象与性质,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.某几何体的三视图如图所示,则该几何体的体积是( )
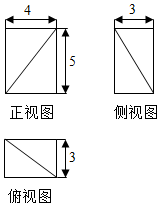

| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
14.过点P(1,2)且倾斜角是直线x-y-3=0的倾斜角的两倍的直线的方程是( )
| A. | x-2y=0 | B. | x=1 | C. | x-2y-4=0 | D. | y=2 |
11.已知菱形的两邻边$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,其对角线交点为D,则$\overrightarrow{OD}$等于( )
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$+$\overrightarrow{b}$ |
8.已知在边长为1的正方形ABCD中,E、F分别在线段AB,BC上运动,若EF=1,则$\overrightarrow{EC}$$•\overrightarrow{FD}$的取值范围是( )
| A. | [1-$\sqrt{2}$,0] | B. | [0,$\sqrt{2}$+1] | C. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+1] |
12.α是第四象限角,cosα=$\frac{12}{13}$,则sin(20kπ-α)=( )
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
7.若(ax2+x+y)5的展开式的各项系数和为243,则x5y2的系数为( )
| A. | 10 | B. | 20 | C. | 30 | D. | 60 |