题目内容
15.正方体ABCD-A1B1C1D1的棱长为3,P是平面AB1D1内一点,满足A1P=$\sqrt{5}$,Q是平面BC1D内异于B的一点,则直线A1P与直线BQ所成角的余弦值的取值范围为[0,$\frac{\sqrt{10}}{5}$].分析 可得点P的轨迹是:在面AB1D1内以O为圆心,半径为$\sqrt{2}$的圆.
由BQ∥面AB1D1内,得直线A1P与直线BQ所成角就是A1P与面AB1D1内直线所成角.
所成角的最小值为斜线A1P与面AB1D1所成角,根据异面直线所成角定义,直线A1P与直线BQ所成角的最大值为$\frac{π}{2}$.即可求解
解答 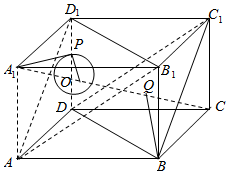 解:如图,连接A1C交面AB1D1内一点O,易得A1O⊥平面AB1D1,${A}_{1}O=\frac{1}{3}{A}_{1}C=\sqrt{3}$
解:如图,连接A1C交面AB1D1内一点O,易得A1O⊥平面AB1D1,${A}_{1}O=\frac{1}{3}{A}_{1}C=\sqrt{3}$
∵P是平面AB1D1内一点,满足A1P=$\sqrt{5}$,∴点P的轨迹是:在面AB1D1内以O为圆心,半径为$\sqrt{2}$的圆.
∵BQ∥面AB1D1内,∴直线A1P与直线BQ所成角就是A1P与面AB1D1内直线所成角.
所成角的最小值为斜线A1P与面AB1D1所成角,∠A1PO,cos$∠{A}_{1}PO=\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5}$
根据异面直线所成角定义,直线A1P与直线BQ所成角的最大值为$\frac{π}{2}$.
直线A1P与直线BQ所成角的余弦值的取值范围为[0,$\frac{\sqrt{10}}{5}$],
故答案为:[0,$\frac{\sqrt{10}}{5}$].
点评 本题考查了空间线面位置关系,异面直线夹角的求解,考查了空间想象能力,属于中档题

练习册系列答案
相关题目
5.6个人排成一排,对排位顺序有如下要求,甲不能排在第一位,乙必须排在前两位,丙必须排在最后一位,那这样排位方法有( )种.
| A. | 54种 | B. | 48种 | C. | 42种 | D. | 36种 |
4.异面直线l与m所成的角为60°,异面直线l与n所成的角为45°,则异面直线m与n所成的角θ的范围是( )
| A. | 15°≤θ≤90° | B. | 60°≤θ≤90° | C. | 15°≤θ≤105° | D. | 30°≤θ≤105° |