题目内容
10.已知m∈R,要使函数f(x)=|x2-4x+9-2m|+2m在区间[0,4]上的最大值是9,则m的取值范围是(-∞,$\frac{7}{2}$].分析 将f(x)配方,求得对称轴,求得f(2),f(0)=f(4),由二次函数的最值取得,可能在顶点处或两端点处,分别计算即可得到所求范围.
解答 解:函数f(x)=|x2-4x+9-2m|+2m
=|(x-2)2+5-2m|+2m,
对称轴为x=2,可得
f(0)=f(4)=|9-2m|+2m,
f(2)=|5-2m|+2m,
由f(x)在区间[0,4]上的最大值是9,
①当f(2)=9,即|5-2m|+2m=9,
解得m=$\frac{7}{2}$,
即f(x)═|(x-2)2-2|+7,
此时f(0)=f(4)=9成立;
②当f(0)=f(4)=|9-2m|+2m=9,
可得9-2m≥0,即m≤$\frac{9}{2}$,
f(2)=|5-2m|+2m≤9,
解得m≤$\frac{7}{2}$,
综上可得m的取值范围是(-∞,$\frac{7}{2}$].
故答案为:(-∞,$\frac{7}{2}$].
点评 本题考查函数的最值的求法,考查分类讨论思想方法,以及二次函数的最值求法,考查运算能力,属于中档题.

练习册系列答案
相关题目
18.设集合A={x|x<0或x>3},B={x||x|<2},则A∩B=( )
| A. | (0,2) | B. | (-2,3) | C. | (-2,0) | D. | (2,3) |
5.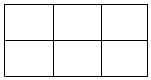 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )| A. | 208 | B. | 204 | C. | 200 | D. | 196 |
2.随着移动互联网时代的到来,手机的使用非常普遍,“低头族”随处可见.某校为了解家长和教师对学生带手机进校园的态度,随机调查了100位家长和教师,得到情况如下表:
(1)是否有95%以上的把握认为“带手机进校园与身份有关”,并说明理由;
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 教师 | 家长 | |
| 反对 | 40 | 20 |
| 支持 | 20 | 20 |
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
20.若角600°的终边上有一点(a,-3),则a的值是( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | -$\frac{{\sqrt{3}}}{3}$ |