题目内容
5.某校共有高中、初中、小学学生4000名,其中小学生1600名,初中生人数是高中生人数的2倍,现用分层抽样的方法抽取一个样本来调查学生每天的课外阅读量.已知样本中小学生共有32人,则该样本中,高中生的人数是16.分析 根据全部学生的人数和小学学生的人数,得到高中、初中共有的人数,根据两个年级人数之间的关系,得到高中生人数,根据小学生人数和小学生抽取的人数,得到概率,用高中生的人数乘以概率得到结果.
解答 解:∵某校共有高中、初中、小学学生4000名,其中小学生1600名,
∴高中、初中共有4000-1600=2400,
∵初中生人数是高中生人数的2倍.
∴高中生有800人,
用分层抽样方法进行调查,样本中小学生共有32人,
每个个体被抽到的概率是$\frac{32}{1600}$=$\frac{1}{50}$
则该样本中的高中生人数为800×$\frac{1}{50}$=16
故答案为:16
点评 本题考查分层抽样方法,考查分层抽样的过程中,每个个体被抽到的概率是相等的,这是解决分层抽样问题的主要依据.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.若角600°的终边上有一点(a,-3),则a的值是( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | -$\frac{{\sqrt{3}}}{3}$ |
14.射击项目选拔赛,四人的平均成绩和方差如下表所示:
从这四个人中选择一人参加该射击项目比赛,最佳人选是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均环数$\overline{x}$ | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差s2 | 3.5 | 3.6 | 2.2 | 5.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,求此点取自黑色部分的概率.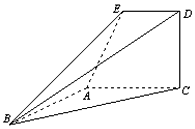 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.