题目内容
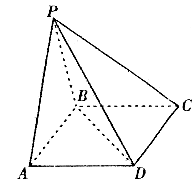
(本题满分12分)如图,四棱锥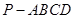 的底面
的底面 是矩形,
是矩形,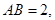
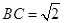 ,且侧面
,且侧面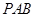 是正三角形,平面
是正三角形,平面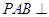 平面
平面 ,
,
(Ⅰ)求证: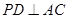 ;
;
(Ⅱ)在棱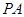 上是否存在一点
上是否存在一点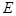 ,使得二面角
,使得二面角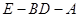 的大小为45°.若存在,试求
的大小为45°.若存在,试求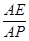 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
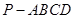 的底面
的底面 是矩形,
是矩形,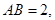
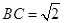 ,且侧面
,且侧面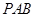 是正三角形,平面
是正三角形,平面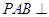 平面
平面 ,
,
(Ⅰ)求证:
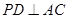 ;
;(Ⅱ)在棱
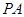 上是否存在一点
上是否存在一点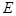 ,使得二面角
,使得二面角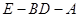 的大小为45°.若存在,试求
的大小为45°.若存在,试求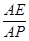 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(Ⅰ)证明见解析;
(Ⅱ)在棱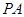 上存在点
上存在点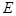 ,当
,当 时,使得二面角
时,使得二面角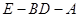 的大小等于45°
的大小等于45°
(Ⅱ)在棱
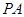 上存在点
上存在点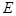 ,当
,当 时,使得二面角
时,使得二面角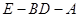 的大小等于45°
的大小等于45° 本试题主要是考查了线线垂直的证明,以及二面角的求解的综合运用。
(1)根据已知条件可得,线面垂直判定定理可以得到线线垂直的证明。
(2)需要合理建立空间直角坐标系,然后设出两个半平面的法向量,然后借助于向量的数量积公式,表示得到向量的夹角,然后利用相等或者互补得到结论。
解:取 中点
中点 ,则由
,则由 ,得
,得 ,又平面
,又平面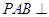 平面
平面 ,且平面
,且平面 平面
平面 ,所以
,所以 平面
平面 .以
.以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 (如图).
(如图).

则
 ……………………2分
……………………2分
(Ⅰ)证明:∵
……………………………………………………………………4分
∴ ,
,
∴ ,即
,即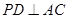 .…………………………………6分
.…………………………………6分
(Ⅱ)假设在棱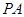 上存在一点
上存在一点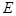 ,不妨设
,不妨设
 ,
,
则点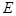 的坐标为
的坐标为 ,……………………………8分
,……………………………8分
∴
设 是平面
是平面 的法向量,则
的法向量,则

不妨取 ,则得到平面
,则得到平面 的一个法向量
的一个法向量 .………10分
.………10分
又面 的法向量可以是
的法向量可以是
要使二面角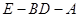 的大小等于45°,
的大小等于45°,
则 45°=
45°=
可解得 ,即
,即
故在棱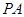 上存在点
上存在点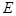 ,当
,当 时,使得二面角
时,使得二面角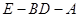 的大小等于45° …12分
的大小等于45° …12分
(1)根据已知条件可得,线面垂直判定定理可以得到线线垂直的证明。
(2)需要合理建立空间直角坐标系,然后设出两个半平面的法向量,然后借助于向量的数量积公式,表示得到向量的夹角,然后利用相等或者互补得到结论。
解:取
 中点
中点 ,则由
,则由 ,得
,得 ,又平面
,又平面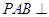 平面
平面 ,且平面
,且平面 平面
平面 ,所以
,所以 平面
平面 .以
.以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 (如图).
(如图).
则
 ……………………2分
……………………2分(Ⅰ)证明:∵

……………………………………………………………………4分
∴
 ,
,∴
 ,即
,即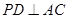 .…………………………………6分
.…………………………………6分(Ⅱ)假设在棱
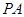 上存在一点
上存在一点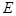 ,不妨设
,不妨设 ,
,则点
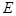 的坐标为
的坐标为 ,……………………………8分
,……………………………8分∴

设
 是平面
是平面 的法向量,则
的法向量,则
不妨取
 ,则得到平面
,则得到平面 的一个法向量
的一个法向量 .………10分
.………10分又面
 的法向量可以是
的法向量可以是
要使二面角
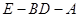 的大小等于45°,
的大小等于45°,则
 45°=
45°=
可解得
 ,即
,即
故在棱
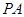 上存在点
上存在点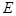 ,当
,当 时,使得二面角
时,使得二面角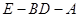 的大小等于45° …12分
的大小等于45° …12分
练习册系列答案
相关题目
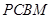 是直角梯形,
是直角梯形,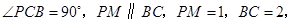 又
又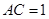 ,
,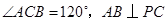 ,直线
,直线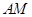 与直线
与直线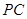 所成的角为
所成的角为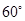 .
.
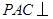 平面
平面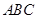 ;
;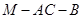 的大小;
的大小;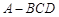 中,
中, 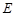 是
是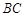 的中点,
的中点,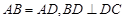
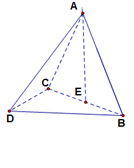
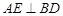 ;
;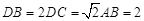 ,且二面角
,且二面角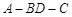 为
为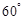 ,求
,求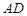 与面
与面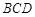 所成角的正弦值。
所成角的正弦值。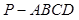 的底面
的底面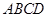 是正方形,侧棱
是正方形,侧棱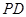 ⊥底面
⊥底面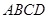 ,
,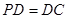 ,
,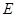 是
是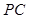 的中点.
的中点. 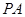 //平面
//平面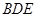 ;
; 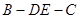 的平面角的余弦值;
的平面角的余弦值;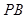 上是否存在点
上是否存在点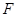 ,使
,使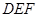 ?若存在,请求出
?若存在,请求出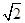 .
. ,PD⊥BC。
,PD⊥BC。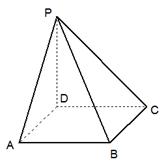
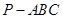 中,
中,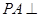 底面
底面 ,
,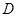 ,
,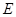 分别在棱
分别在棱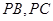 上,且
上,且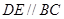
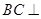 平面
平面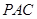 ;
;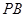 的中点时,求
的中点时,求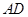 与平面
与平面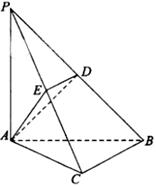
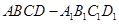 的底面边长为
的底面边长为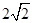 ,
,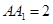 ,点
,点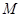 是
是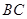 的中点,
的中点,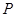 是平面
是平面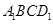 内的一个动点,且满足
内的一个动点,且满足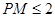 ,
,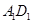 和
和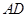 的距离相等,则点
的距离相等,则点
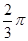
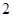
 、
、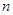 ,平面
,平面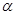 、
、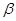 ,给出下列命题:
,给出下列命题: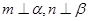 ,且
,且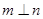 ,则
,则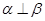 ②若
②若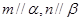 ,且
,且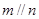 ,则
,则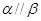
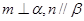 ,且
,且