题目内容
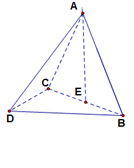
三棱锥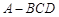 中,
中, 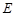 是
是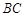 的中点,
的中点,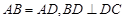
(I)求证: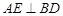 ;
;
(II)若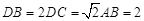 ,且二面角
,且二面角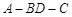 为
为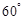 ,求
,求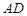 与面
与面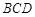 所成角的正弦值。
所成角的正弦值。
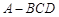 中,
中, 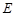 是
是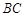 的中点,
的中点,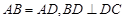

(I)求证:
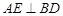 ;
;(II)若
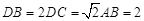 ,且二面角
,且二面角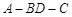 为
为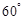 ,求
,求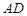 与面
与面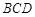 所成角的正弦值。
所成角的正弦值。(I)见解析;(II) 。
。
 。
。本试题主要是考查了立体几何总空间中的线线垂直的证明以及线面角的求解的综合运用。
(1)对于线线的垂直的证明,主要利用线面垂直的性质定理得到,先分先要证明的线和平面,然后找突破口进而求证。
(2)而对于线面角的求解问题,既可以采用向量法,也可以采用得到斜线和斜线在平面内的射影,借助于线面角的定义作出角,分析求解。
解:(I)如图取 的中点
的中点 ,连
,连 ,
,

∵ 为
为 中点,
中点, 为
为 中点,∴
中点,∴ .
.
 ∴
∴ .
.
∵ ∴
∴
又 ,
,
∴ …………4分
…………4分
∵ ,∴
,∴ …………6分
…………6分
(II)由(I)知 ,
,
 。
。

 …………8分
…………8分

 ,
,
 为等腰直角三角形,
为等腰直角三角形, ,
,


 …………10分
…………10分
又由(1)知


 就是
就是 与面
与面 所成角 , …………12分
所成角 , …………12分
在 中,
中, ,
,

 .
.
即直线 与面
与面 所成角的正弦值为
所成角的正弦值为 …………14分
…………14分
(1)对于线线的垂直的证明,主要利用线面垂直的性质定理得到,先分先要证明的线和平面,然后找突破口进而求证。
(2)而对于线面角的求解问题,既可以采用向量法,也可以采用得到斜线和斜线在平面内的射影,借助于线面角的定义作出角,分析求解。
解:(I)如图取
 的中点
的中点 ,连
,连 ,
,
∵
 为
为 中点,
中点, 为
为 中点,∴
中点,∴ .
.  ∴
∴ .
. ∵
 ∴
∴
又
 ,
,
∴
 …………4分
…………4分∵
 ,∴
,∴ …………6分
…………6分(II)由(I)知
 ,
,
 。
。
 …………8分
…………8分
 ,
,
 为等腰直角三角形,
为等腰直角三角形, ,
,


 …………10分
…………10分又由(1)知



 就是
就是 与面
与面 所成角 , …………12分
所成角 , …………12分在
 中,
中, ,
,

 .
.即直线
 与面
与面 所成角的正弦值为
所成角的正弦值为 …………14分
…………14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
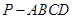 中,
中, 底面
底面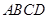 ,四边形
,四边形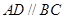 ,
, ,
, ,
,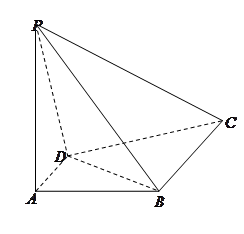
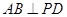 ;
;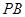 上找出一点
上找出一点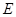 ,使
,使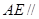 平面
平面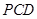 ,
,
 面ABC,BC
面ABC,BC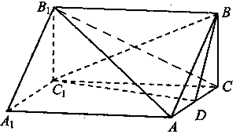
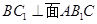 ;
;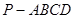 中,
中,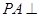 平面
平面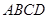 ,底面
,底面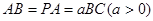 .
.
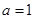 时,求证:
时,求证: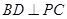 ;
;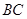 边上有且只有一个点
边上有且只有一个点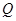 ,使得
,使得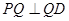 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.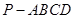 的底面
的底面 是矩形,
是矩形,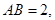
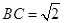 ,且侧面
,且侧面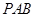 是正三角形,平面
是正三角形,平面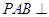 平面
平面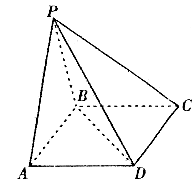
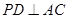 ;
;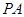 上是否存在一点
上是否存在一点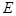 ,使得二面角
,使得二面角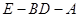 的大小为45°.若存在,试求
的大小为45°.若存在,试求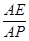 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.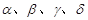 表示平面,
表示平面,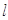 为直线,下列命题中为真命题的是 ( )
为直线,下列命题中为真命题的是 ( )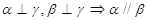
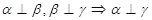
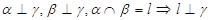
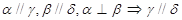
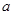 、
、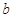 、
、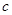 表示三条不同的直线,
表示三条不同的直线,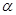 表示平面,给出下列命题:
表示平面,给出下列命题: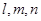 是三条不同的直线,
是三条不同的直线,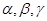 是三个不同的平面,现给出四个命题:
是三个不同的平面,现给出四个命题: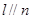 且
且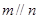 ,则
,则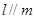 ; ②若
; ②若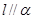 且
且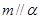 ,则
,则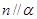 且
且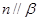 ,则
,则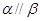 ; ④若
; ④若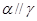 且
且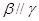 ,则
,则