题目内容
(本小题满分12分)
如图,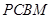 是直角梯形,
是直角梯形,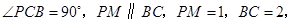 又
又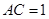 ,
,
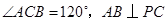 ,直线
,直线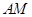 与直线
与直线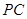 所成的角为
所成的角为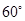 .
.

(Ⅰ)求证:平面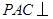 平面
平面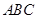 ;
;
(Ⅱ)求二面角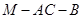 的大小;
的大小;
如图,
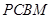 是直角梯形,
是直角梯形,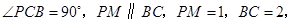 又
又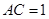 ,
,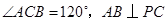 ,直线
,直线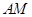 与直线
与直线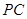 所成的角为
所成的角为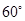 .
.
(Ⅰ)求证:平面
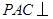 平面
平面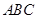 ;
;(Ⅱ)求二面角
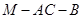 的大小;
的大小;(Ⅰ)见解析;(Ⅱ)
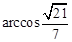 或
或 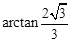 。
。(I)证明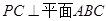 即可.
即可.
(II) 取BC的中点N,连结AN,MN,可证出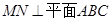 ,
,
再作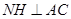 ,交AC的延长线于H,连结MH,则由三垂线定理知,
,交AC的延长线于H,连结MH,则由三垂线定理知,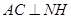 ,
,
从而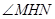 为二面角
为二面角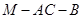 的平面角 ,然后解三角形求角即可.
的平面角 ,然后解三角形求角即可.
解法一:
(Ⅰ)∵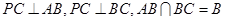
∴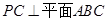 ,
,
又∵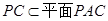
∴ …………5分
…………5分
(Ⅱ)取 的中点
的中点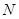 ,则
,则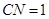 ,连结
,连结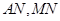 ,
,
∵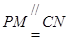 ,∴
,∴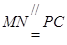 ,从而
,从而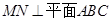
作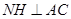 ,交
,交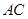 的延长线于
的延长线于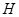 ,连结
,连结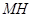 ,则由三垂线定理知,
,则由三垂线定理知,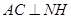 ,
,
从而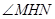 为二面角
为二面角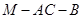 的平面角 …………8分
的平面角 …………8分
直线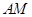 与直线
与直线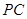 所成的角为
所成的角为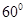
∴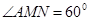
在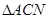 中,由余弦定理得
中,由余弦定理得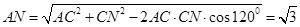
在 中,
中,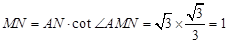
在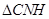 中,
中,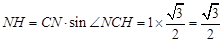
在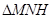 中,
中,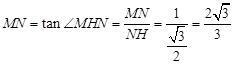
故二面角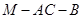 的平面角大小为
的平面角大小为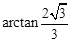 …………12分
…………12分
解法二:(Ⅰ)同解法一
(Ⅱ)在平面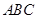 内,过
内,过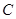 作
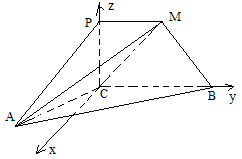
作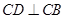 ,建立空间直角坐标系
,建立空间直角坐标系 (如图)
(如图)
由题意有 ,设
,设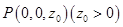 ,
,
则
由直线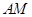 与直线
与直线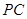 所成的解为
所成的解为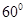 ,得
,得
 ,即
,即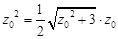 ,解得
,解得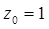
∴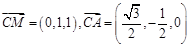 ,设平面
,设平面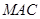 的一个法向量为
的一个法向量为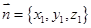 ,
,
则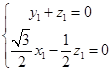 ,取
,取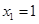 ,得
,得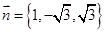 …………8分
…………8分
平面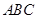 的法向量取为
的法向量取为
设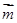 与
与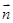 所成的角为
所成的角为 ,则
,则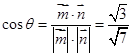
显然,二面角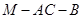 的平面角为锐角,
的平面角为锐角,
故二面角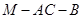 的平面角大小为
的平面角大小为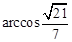 …………12分
…………12分
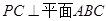 即可.
即可.(II) 取BC的中点N,连结AN,MN,可证出
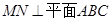 ,
,再作
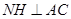 ,交AC的延长线于H,连结MH,则由三垂线定理知,
,交AC的延长线于H,连结MH,则由三垂线定理知,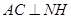 ,
,从而
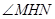 为二面角
为二面角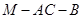 的平面角 ,然后解三角形求角即可.
的平面角 ,然后解三角形求角即可.解法一:
(Ⅰ)∵
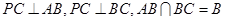
∴
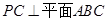 ,
,又∵
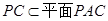
∴
 …………5分
…………5分(Ⅱ)取
 的中点
的中点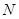 ,则
,则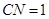 ,连结
,连结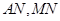 ,
,∵
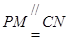 ,∴
,∴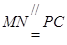 ,从而
,从而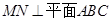
作
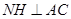 ,交
,交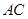 的延长线于
的延长线于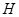 ,连结
,连结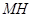 ,则由三垂线定理知,
,则由三垂线定理知,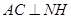 ,
,从而
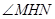 为二面角
为二面角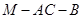 的平面角 …………8分
的平面角 …………8分直线
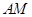 与直线
与直线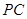 所成的角为
所成的角为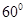
∴
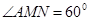
在
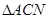 中,由余弦定理得
中,由余弦定理得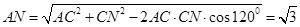
在
 中,
中,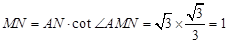
在
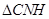 中,
中,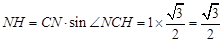
在
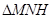 中,
中,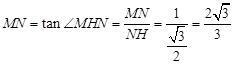
故二面角
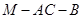 的平面角大小为
的平面角大小为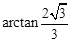 …………12分
…………12分解法二:(Ⅰ)同解法一
(Ⅱ)在平面
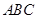 内,过
内,过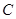 作
作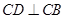 ,建立空间直角坐标系
,建立空间直角坐标系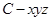 (如图)
(如图)
由题意有
 ,设
,设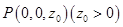 ,
,则

由直线
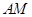 与直线
与直线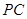 所成的解为
所成的解为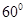 ,得
,得 ,即
,即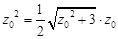 ,解得
,解得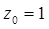
∴
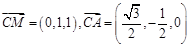 ,设平面
,设平面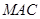 的一个法向量为
的一个法向量为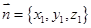 ,
,则
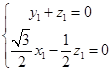 ,取
,取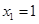 ,得
,得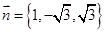 …………8分
…………8分平面
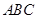 的法向量取为
的法向量取为
设
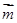 与
与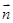 所成的角为
所成的角为 ,则
,则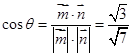
显然,二面角
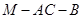 的平面角为锐角,
的平面角为锐角,故二面角
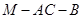 的平面角大小为
的平面角大小为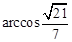 …………12分
…………12分
练习册系列答案
相关题目
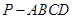 中,
中, 底面
底面 ,四边形
,四边形 ,
, ,
, ,
,
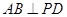 ;
;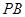 上找出一点
上找出一点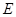 ,使
,使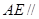 平面
平面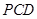 ,
,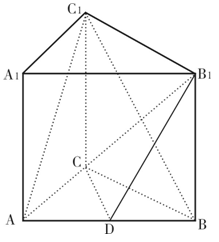

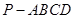 的底面
的底面 是矩形,
是矩形,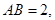
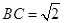 ,且侧面
,且侧面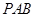 是正三角形,平面
是正三角形,平面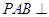 平面
平面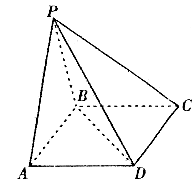
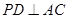 ;
;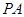 上是否存在一点
上是否存在一点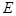 ,使得二面角
,使得二面角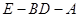 的大小为45°.若存在,试求
的大小为45°.若存在,试求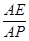 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.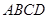 中,
中,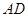 ⊥面
⊥面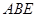 ,
,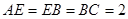 ,
,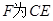 上的点,且
上的点,且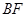 ⊥面
⊥面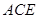 ,
,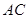 、
、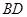 交于点
交于点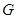 .
.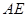 ⊥
⊥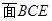 ;
;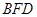 .
.
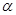 和直线l,则
和直线l,则