题目内容
具有性质:f(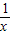 )=-f(x)的函数,我们称为满足“倒负”变换的函数数,下列函数①y=x-
)=-f(x)的函数,我们称为满足“倒负”变换的函数数,下列函数①y=x-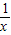 ②y=x+
②y=x+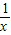 ③y=
③y=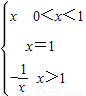 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )A.①②
B.①③
C.②
D.只有①
【答案】分析:利用“倒负”函数定义,分别比较三个函数的f(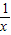 )与-f(x)的解析式,若符合定义,则为满足“倒负”变换的函数,若不符合,则举反例说明函数不符合定义,从而不是满足“倒负”变换的函数
)与-f(x)的解析式,若符合定义,则为满足“倒负”变换的函数,若不符合,则举反例说明函数不符合定义,从而不是满足“倒负”变换的函数
解答:解:①设f(x)=x-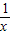 ,∴f(
,∴f(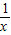 )=
)=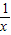 -
-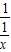 =
=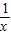 -x=-f(x),∴y=x-
-x=-f(x),∴y=x-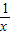 是满足“倒负”变换的函数
是满足“倒负”变换的函数
②设f(x)=x+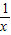 ,∵f(
,∵f( )=
)= ,-f(2)=-
,-f(2)=- ,即f(
,即f( )≠-f(2),∴y=x+
)≠-f(2),∴y=x+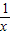 是不满足“倒负”变换的函数
是不满足“倒负”变换的函数
③设f(x)=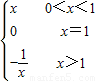 则-f(x)=
则-f(x)=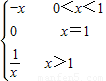
∵0<x<1时,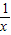 >1,此时f(
>1,此时f(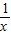 )=-
)=-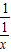 =-x;
=-x;
x=1时,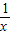 =1,此时f(
=1,此时f(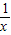 )=0
)=0
x>1时,0<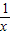 <1,此时f(
<1,此时f(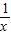 )=
)=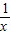
∴f(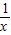 )=
)=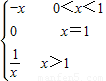 =-f(x),
=-f(x),
∴y=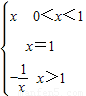 是满足“倒负”变换的函数
是满足“倒负”变换的函数
故选 B
点评:本题考查了对新定义函数的理解,复合函数解析式的求法,分段函数解析式的求法
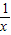 )与-f(x)的解析式,若符合定义,则为满足“倒负”变换的函数,若不符合,则举反例说明函数不符合定义,从而不是满足“倒负”变换的函数
)与-f(x)的解析式,若符合定义,则为满足“倒负”变换的函数,若不符合,则举反例说明函数不符合定义,从而不是满足“倒负”变换的函数解答:解:①设f(x)=x-
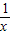 ,∴f(
,∴f(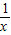 )=
)=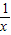 -
-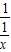 =
=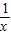 -x=-f(x),∴y=x-
-x=-f(x),∴y=x-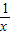 是满足“倒负”变换的函数
是满足“倒负”变换的函数②设f(x)=x+
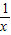 ,∵f(
,∵f( )=
)= ,-f(2)=-
,-f(2)=- ,即f(
,即f( )≠-f(2),∴y=x+
)≠-f(2),∴y=x+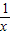 是不满足“倒负”变换的函数
是不满足“倒负”变换的函数③设f(x)=
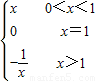 则-f(x)=
则-f(x)=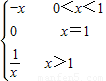
∵0<x<1时,
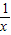 >1,此时f(
>1,此时f(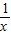 )=-
)=-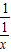 =-x;
=-x;x=1时,
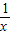 =1,此时f(
=1,此时f(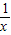 )=0
)=0x>1时,0<
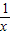 <1,此时f(
<1,此时f(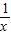 )=
)=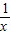
∴f(
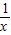 )=
)=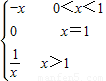 =-f(x),
=-f(x),∴y=
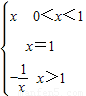 是满足“倒负”变换的函数
是满足“倒负”变换的函数故选 B
点评:本题考查了对新定义函数的理解,复合函数解析式的求法,分段函数解析式的求法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目