题目内容
5.设命题p:?n∈N,n2≤2n,则¬p为( )| A. | ?n∈N,n2>2n | B. | ?n∈N,n2≤2n | C. | ?n∈N,n2>2n | D. | ?n∈N,n2≥2n |
分析 利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题P:?n∈N,n2≤2n,则¬P为:?n∈N,n2>2n.
故选:C.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知某几何体的三视图如图所示,则该几何体的体积是( )
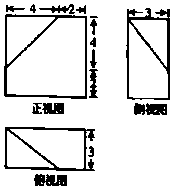

| A. | 100 | B. | 82 | C. | 96 | D. | 112 |
20.半径为2的球内有一底面边长为2的内接正四棱柱(底面是正方形,侧棱垂直底面),则当该正四棱柱的侧面积最大时球的表面积与该正四棱柱的侧面积之差是( )
| A. | $16({π-\sqrt{3}})$ | B. | $16({π-\sqrt{2}})$ | C. | $8({2π-3\sqrt{2}})$ | D. | $8({2π-\sqrt{3}})$ |
10.cos135°的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |