题目内容
已知函数f(x)=k(x-1)ex+x2.
(1)当k=- 时,求函数f(x)在点(1,1)处的切线方程;
时,求函数f(x)在点(1,1)处的切线方程;
(2)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(3)当k≤-1时,求函数f(x)在[k,1]上的最小值m.
【解】 (1)当k=- 时,f(x)=-
时,f(x)=- (x-1)ex+x2,f′(x)=-xex-1+2x,f′(1)=1
(x-1)ex+x2,f′(x)=-xex-1+2x,f′(1)=1 ,
,
函数f(x)在点(1,1)处的切线方程为y=x.
(2)f′(x)=kx <x2+(k+2)x,
<x2+(k+2)x,
即kxex-x2-kx<0.
因为x<0,所以kex-x-k>0,
令h(x)=kex-x-k,则h′(x)=kex-1.
当k≤0时,h(x)在(-∞,0)上为减函数,h(x)>h(0)=0,符合题意;
当0<k≤1时,h(x)在(-∞,0)上为减函数,h(x)>h(0)=0,符合题意
当k>1时,h(x)在(-∞,-ln k)上为减函数,在(-ln k,0)上为增函数,h(-ln k)<h(0)=0,不合题意.
综上:k≤1.


练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,则
,则 B.若
B.若 ,则
,则
 ,则
,则 D.若
D.若 ,则
,则
 对任意实数x均成立,则实数a的取值范围为____.
对任意实数x均成立,则实数a的取值范围为____.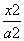 -
- =1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲
=1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲 线渐近线的一个交点为(3,4),则此双曲线的方程为( )
线渐近线的一个交点为(3,4),则此双曲线的方程为( )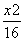 -
- =1 B.
=1 B.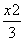 -
-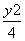 =1
=1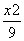 -
-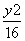 =1 D.
=1 D.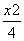 -
-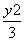 =1
=1 上的一点向圆
上的一点向圆 引切线,则切线长的
引切线,则切线长的 C.
C. D.3
D.3
 图象的一条对称轴是直线
图象的一条对称轴是直线
 ;
; 上的图象(不必写出作图步骤).
上的图象(不必写出作图步骤).
 ,则
,则 等于( )
等于( )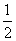 B.1 C.2 D.3
B.1 C.2 D.3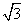 cos(2x+φ)+sin(2x+φ)
cos(2x+φ)+sin(2x+φ)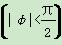 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )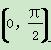 上为增函数
上为增函数 上为增函数
上为增函数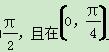 上为减函数
上为减函数