题目内容
18．已知a，b∈R，i是虚数单位，若（2+i）（1-bi）=a+i，则a+b=2．分析 直接由复数代数形式的乘法运算化简（2+i）（1-bi），再由复数相等的条件列出方程组，求解即可得答案．
解答 解：由（2+i）（1-bi）=（2+b）+（1-2b）i=a+i，
则$\left\{\begin{array}{l}{2+b=a}\\{1-2b=1}\end{array}\right.$，
解得a=2，b=0．
则a+b=2．
故答案为：2．
点评 本题考查了复数代数形式的乘法运算，考查了复数相等的条件，是基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
8．
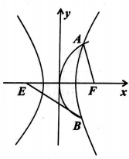已知E，F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（0＜a＜b）的左右焦点，抛物线y2=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于A，B不同两地两点，若|AF|=$\frac{4}{5}$|BE|，则双曲线的离心率为（ ）
已知E，F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（0＜a＜b）的左右焦点，抛物线y2=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于A，B不同两地两点，若|AF|=$\frac{4}{5}$|BE|，则双曲线的离心率为（ ）| A． | 4-$\sqrt{7}$ | B． | 4-$\sqrt{3}$ | C． | 4+$\sqrt{3}$ | D． | 4+$\sqrt{7}$ |
6．在△ABC中，“A=B”是“sinAcosA=sinBcosB”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
13．某企业生产A、B两种产品，它们的原料中均含甲、乙两种溶液，生产每件产品所需两种溶液的剂量如下表所示：
生产产品A和B每件分别获得利润2万元、3万元，现只有甲、乙两种溶液各60升，该企业有三种生产方案，方案一：只生产A．方案二：只生产B．方案三：按一定比例生产A、B实现利润最大化．
（1）方案一和方案二中哪种方案利润较高；
（2）按照方案三生产，则产品A、B各生产多少件，最大利润为多少，判断方案三是否优于方案一和方案二．
| 单位：升 | A | B |
| 甲 | 4 | 2 |
| 乙 | 1 | 5 |
（1）方案一和方案二中哪种方案利润较高；
（2）按照方案三生产，则产品A、B各生产多少件，最大利润为多少，判断方案三是否优于方案一和方案二．
7．设数列{an}的前n项和为Sn，且a1=$\frac{1}{2}$，{Sn+nan}为常数列，则an=（ ）
| A． | $\frac{1}{n（n+1）}$ | B． | $\frac{1}{{2}^{n}}$ | C． | $\frac{3}{（n+1）（n+2）}$ | D． | $\frac{5-2n}{6}$ |
8．在等差数列{an}中，a3+a6=a4+5，且a2不大于1，则a8的取值范围是（ ）
| A． | （-∞，9] | B． | [9，+∞） | C． | （-∞，9） | D． | （9，+∞） |