题目内容
6．在△ABC中，“A=B”是“sinAcosA=sinBcosB”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 由sinAcosA=sinBcosB，可得：sin2A=sin2B，由于A，B∈（0，π），可得2A=2B，或2A+2B=π，即可判断出结论．
解答 解：由sinAcosA=sinBcosB，可得：sin2A=sin2B，
∵A，B∈（0，π），∴2A=2B，或2A+2B=π，即A=B，或A+B=$\frac{π}{2}$，
∴“A=B”是“sinAcosA=sinBcosB”的充分不必要条件．
故选：A．
点评 本题考查了倍角公式、三角函数求值、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
16．曲线y=a$\sqrt{x}$（a＞0）与曲线y=ln$\sqrt{x}$有公共点，且在公共点处的切线相同，则a的值为（ ）
| A． | e | B． | e2 | C． | e-2 | D． | e-1 |
14．已知复数z满足z=$\frac{5}{2-i}$，则|z|=（ ）
| A． | 2 | B． | $\sqrt{5}$ | C． | 3 | D． | 5 |
1．已知M为△ABC内一点，$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$，则△ABM和△ABC的面积之比为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
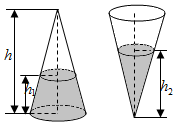如图，圆锥形容器的高为h，圆锥内水面的高为h1，且$\frac{h_1}{h}$=$\frac{1}{3}$，若将圆锥倒置，水面高为h2，则$\frac{h_2}{h}$等于$\frac{\root{3}{19}}{3}$．