题目内容
已知△ABC，点M满足
+2
=3
，则△ABM与△ABC的面积之比为 ．
| AB |
| AC |
| AM |
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：由向量的运算可得M为CB的三等分点，由三角形的面积公式可得．
解答：
解：∵
+2
=3
，∴
-
+2
=3
-
，
∴
-
=3（
-
），∴
=3
，
∴M为CB的三等分点，（靠近C），
设△ABC的边BC边上的高为h，
则△ABM的面积为
BM•h，△ABC的面积为
AB•h，
∴△ABM与△ABC的面积之比为BM：AB=2：3
故答案为：2：3．
| AB |
| AC |
| AM |
| AB |
| AC |
| AC |
| AM |
| AC |
∴
| AB |
| AC |
| AM |
| AC |
| CB |
| CM |
∴M为CB的三等分点，（靠近C），
设△ABC的边BC边上的高为h，
则△ABM的面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABM与△ABC的面积之比为BM：AB=2：3
故答案为：2：3．
点评：本题考查向量的运算，得出M为CB的三等分点是解决问题的关键，属基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
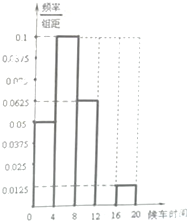常州公交公司为了调整302线路发车的时间间隔，在某站点对乘客进行了候车时间的调查，以下是候车时间的频率分布表和频率分布直方图．
如图，为了估计阴影部分的面积，向边长为6的正方形内随机投掷800个点，恰有200个点落在阴影部分内，据此，可估计阴影部分的面积为“m=3”是“椭圆
+
=1的离心率e=
”的（ ）
| x2 |
| 5 |
| y2 |
| m |
| ||
| 5 |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |