题目内容
16.在△ABC中,内角A,B,C的对边分别是a,b,c,且$\frac{tanA}{tanB}=\frac{2c-b}{b}$.(1)将函数$f(x)=sin({2x+φ})({0<φ<\frac{π}{2}})$的图象向右平移角A个单位可得到函数g(x)=-cos2x的图象,求φ的值;
(2)若△ABC的外接圆半径为1,求△ABC面积的最大值.
分析 (1)根据$\frac{tanA}{tanB}=\frac{2c-b}{b}$利用正弦定理求解出角A大小,根据三角函数图象的平移变换即可求解φ的值.
(2)根据△ABC的外接圆半径为1,利用正弦定理和余弦定理,结合基本不等式可得△ABC面积的最大值.
解答 解:由$\frac{tanA}{tanB}=\frac{2c-b}{b}$和正弦定理可得:$\frac{sinAcosB}{cosAsinB}=\frac{2sinC-sinB}{sinB}$,
整理得:sinAcosB=2sinCcosA-sinBcosA,即sinC=2sinCcosA,
∵sinC≠0,
∴cosA=$\frac{1}{2}$,0<A<π,
∴$A=\frac{π}{3}$.
将函数$f(x)=sin({2x+φ})({0<φ<\frac{π}{2}})$的图象向右平移角A个单位,可得:sin[2(x-$\frac{π}{3}$)+φ].
由题意可得:sin[2(x-$\frac{π}{3}$)+φ]=-cos2x,即sin(2x-$\frac{2π}{3}$+φ)=sin(2x-$\frac{π}{2}$),
∴φ$-\frac{2π}{3}$=$-\frac{π}{2}$+2kπ(k∈Z),
∴φ=$\frac{π}{6}$+2kπ(k∈Z),
∵0<φ$<\frac{π}{2}$,
∴φ=$\frac{π}{6}$.
(2)根据△ABC的外接圆半径为1,A=$\frac{π}{3}$,
∴2RsinA=a,即a=$\sqrt{3}$.
由余弦定理:a2=b2+c2-2bccosA,可得:3=b2+c2-bc,
即3+bc≥2bc,可得bc≤3,当且仅当b=c是取等号.
∴△ABC面积的最大值$S=\frac{1}{2}bcsinA≤\frac{1}{2}×3×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}$.
点评 本题考查了三角函数图象的平移变换,正弦定理和余弦定理,基本不等式等知识点的灵活运用和计算能力.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | {x|x<-1} | B. | {x|x≤-1,或x>2} | C. | {x|x≥2,或x=-1} | D. | {x|x<-1,或x≥2} |
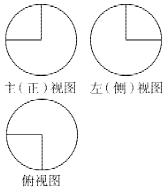 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的表面积是17π,则它的体积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的表面积是17π,则它的体积是( )| A. | 8π | B. | $\frac{56π}{3}$ | C. | $\frac{14π}{3}$ | D. | $\frac{28π}{3}$ |
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
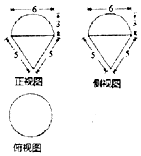
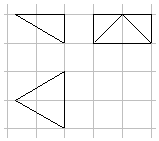 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )| A. | $\frac{19π}{3}$ | B. | $\frac{22π}{3}$ | C. | 19π | D. | 22π |
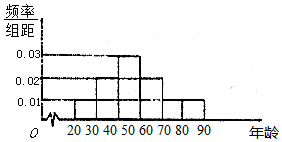 退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.
退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.