题目内容
17.在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且椭圆C上的点到右焦点F的距离的最大值为2$\sqrt{2}$+2.(1)求椭圆C的方程;
(2)过点F且不与x轴垂直或重合的直线l与椭圆C交于M、N两点,问:x轴上是否存在点P,使得∠OPM=∠OPN?若存在,求出点P的坐标;若不存在,说明理由.
分析 (1)由题意知$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{a+c=2\sqrt{2}+2}\end{array}\right.$,从而解得;
(2)假设存在,从而可设直线l的方程为y=k(x-2),联立方程$\left\{\begin{array}{l}{y=k(x-2)}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$化简可得(2k2+1)x2-8k2x+8k2-8=0,从而可得x1+x2=$\frac{8{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{8{k}^{2}-8}{2{k}^{2}+1}$,易知M,N′,P三点共线,从而可得(x1-x0)y2+(x2-x0)y1=0,从而化简可得.
解答 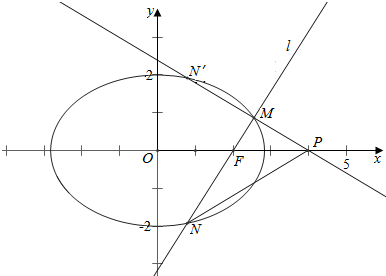 解:(1)由题意知,
解:(1)由题意知,
$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{a+c=2\sqrt{2}+2}\end{array}\right.$,
解得,a=2$\sqrt{2}$,c=2,b=2;
故椭圆C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)假设存在点P,使得∠OPM=∠OPN,由题意,
点F(2,0),设直线l的方程为y=k(x-2),
点N(x1,y1),M(x2,y2),N′(x1,-y1),P(x0,0);
联立方程可得,
$\left\{\begin{array}{l}{y=k(x-2)}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,
化简可得,
(2k2+1)x2-8k2x+8k2-8=0,
故x1+x2=$\frac{8{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{8{k}^{2}-8}{2{k}^{2}+1}$,
∵∠OPM=∠OPN,N与N′关于x轴对称,
∴M,N′,P三点共线,
∵$\overrightarrow{PM}$=(x2-x0,y2),$\overrightarrow{PN′}$=(x1-x0,-y1),
∴(x1-x0)y2+(x2-x0)y1=0,
即(x1-x0)k(x2-2)+(x2-x0)k(x1-2)=0,
即2x1x2-2(x1+x2)+[4-(x1+x2)]x0=0,
即2$\frac{8{k}^{2}-8}{2{k}^{2}+1}$-2$\frac{8{k}^{2}}{2{k}^{2}+1}$+[4-$\frac{8{k}^{2}}{2{k}^{2}+1}$]x0=0,
解得,x0=4,
故点P的坐标为(4,0).
点评 本题考查了椭圆的标准方程的求法及数形结合的思想应用,同时考查了平面向量的应用.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| PM2.5日均浓度(ug/m3) | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
(2)在表数据中、在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度小于75ug/m3”,求事件M发生的概率.
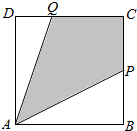 如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.