题目内容
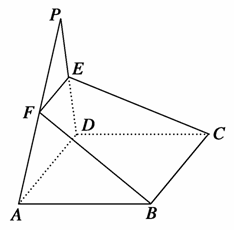
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2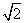 ,∠PAB=60°.M是PD的中点.
,∠PAB=60°.M是PD的中点.
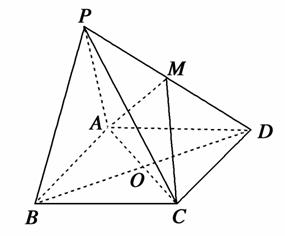
(1)证明:PB∥平面MAC;
(2)证明:平面PAB⊥平面ABCD;
(3)求四棱锥P-ABCD的体积.
[解析] (1)证明:连接OM.
∵M是PD中点,矩形ABCD中O为BD中点,
∴OM∥PB.
又OM平面MAC,PB⃘平面MAC,
∴PB∥平面MAC.
(2)证明:由题设知PA=2,AD=2,PD=2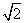 ,
,
有PA2+AD2=PD2,∴AD⊥PA.
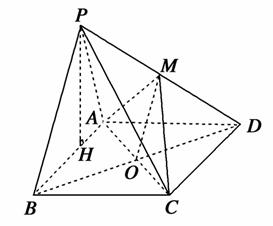
在矩形ABCD中,AD⊥AB.
又PA∩AB=A,∴AD⊥平面PAB.
∵AD平面ABCD,
∴平面PAB⊥平面ABCD.
(3)解:过点P作PH⊥AB于点H.
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PH⊥平面ABCD.
在Rt△PHA中,PH=PAsin60°=2×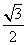 =
=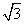 ,
,
VP-ABCD=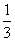 AB×AD×PH=
AB×AD×PH=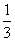 ×3×2×
×3×2×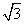 =2
=2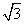 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
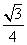 a2 B.
a2 B.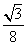 a2 C.
a2 C.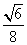 a2 D.
a2 D.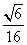 a2
a2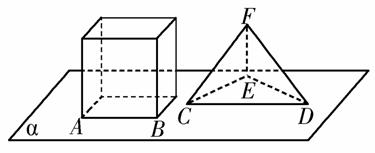
 .
.
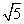 B.4
B.4 D.2
D.2