题目内容
20.关于x的方程x2-(m+3)x+m+3=0有两个不相等的正实数根,则实数m的取值范围是(1,+∞).分析 由已知中关于x的方程x2-(m+3)x+m+3=0有两个不相等的正实数根,则方程的△>0,且方程的两根x1,x2满足x1+x2>0,x1•x2>0,由此构造一个关于m的不等式组,解不等式组即可得到实数m的取值范围.
解答 解:若关于x的方程x2-(m+3)x+m+3=0有两个不相等的正实数根,
即x1>0,x2>0,且x1≠x2,
∴△=(m+3)2-4(m+3)>0且m+3>0,
解得m>1
故实数m的取值范围是(1,+∞).
故答案为:(1,+∞).
点评 本题考查的知识点是一元二次方程的根的分布与系数的关系,韦达定理,其中根据已知条件,结合一元二次方程的根的个数与△的关系及韦达定理,构造一个关于m的不等式组,是解答本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
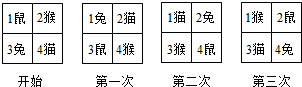
15.四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第202次互换座位后,小兔坐在第2号座位上.

12.若变量x,y满足约束条件$\left\{\begin{array}{l}2x-y≤0\\ x-3y+5≥0\\ y≥1\end{array}\right.$,则${(\frac{1}{2})^{x+y-2}}$的最大值是( )
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |